6. Sınıf Çarpanlar ve Katlar Konu Anlatımı

Çarpanlar ve Katlar, Bölünebilme Kuralları. Asal Sayılar ve Asal Çarpanlar, Ortak Bölenler ve Katlar, 6. Sınıf Çarpanlar ve Katlar Konu Anlatımı, 6. Sınıf Çarpanlar ve Katlar , Çarpanlar ve Katlar Konu Anlatımı, 6. Sınıf Matematik , 6. Sınıf Matematik Konu Anlatımı, Çarpanlar ve Katlar

Çarpanlar ve Katlar

Bir doğal sayı iki doğal sayının çarpımı olarak yazılabilir. Bu iki sayıdan her birine o sayının çarpanı denir. Bir sayının çarpanı aynı zamanda o sayının kalansız bölenidir.

Örnek-1

48 sayısının çarpanlarını (kalansız bölenlerini) bulalım.

48’in iki sayının çarpımı şeklinde yazalım.

48 = 1 x 48
48 = 2 x 24
48 = 3 x 16
48 = 4 x 12
48 = 6 x 8

48 sayısının çarpanları : 1, 2, 3, 4, 6, 8, 12,16, 24, 48.

Örnek-2

50 sayısının çarpanlarını bulalım.

1 . 50 = 50
2 . 25 = 50
5 . 10 = 50

50 sayısının çarpanları: 1, 2, 5, 10, 25, 50.

Bir Doğal Sayının Çarpanları/Bölenleri

Bir doğal sayının kalansız böldüğü sayıların tümüne o sayının katları denir.

Örnek

3’ün katları
3, 6, 9, 12, 15, . . . dir.

Kalansız Bölünebilme

2 ile bölünebilme: Birler basamağında 0, 2, 4, 6 ve 8 rakamlarından biri bulunan sayılar 2 ile kalansız bölünür.

Örnek

456 sayısının birler basamağında 6 rakamı olduğu için bu sayı 2 ile kalansız bölünür.

3 ile bölünebilme: Rakamları toplamı 3’ün katı olan sayılar 3 ile kalansız bölünür.

Örnek

672 sayısının rakamları toplamı 6 + 7 + 2 = 15’dir.

15 sayısı 3’ün katı olduğu için 672 sayısı 3 ile kalansız bölünür.

4 ile bölünebilme: Son iki basamağı “00” veya 4’ün katı olan sayılar 4 ile kalansız bölünür.

Örnek

632 , 300, 544, 288 … sayıları 4 ‘e tam bölünür.

6 ile bölünebilme: Hem 2 hemde 3 ile kalansız bölünen sayılar 6 ile kalansız bölünür.

Örnek

2514 sayısının son basamağındaki rakam “4” olduğu için 2514 sayısı 2 ile kalansız bölünürken rakamları toplamı 2 + 5 + 1 + 4 = 15 sayısında 3’ün katı olduğu için 3 ile kalansız bölünür. Hem 2’ye hemde 3’e bölünen 2514 sayısı 6 ile kalansız bölünür.

5 ile bölünebilme: Birler basamağı “0” veya “5” olan sayılar 5 ile kalansız bölünür.

Örnek

230 sayısının birler basamağında 0 olduğundan 230 sayısı 5 ile kalansız olarak bölünür.

9 ile bölünebilme: Rakamları toplamı 9’un katı olan sayılar 9 ile kalansız bölünür.

Örnek

4185 sayısının rakamları toplamı 4 + 1 + 8 + 5 = 18’dir.

18 sayısı 9’un katı olduğu için 4185 sayısı 9 ile kalansız bölünür.

10 ile Bölünebilme: Bir sayının birler basamağında 0 (sıfır) varsa bu sayı 10 ile tam bölünür.

Örnek

610 sayısının birler basamağındaki rakam 0 olduğundan 610 sayısı 10 ile tam olarak bölünür.

Asal Sayılar ve Asal Çarpanlar

Asal Sayılar

1 ve kendisinden başka böleni olmayan 1’den büyük doğal sayılara asal sayılar denir. 1’den 100’ e kadar olan asal sayılar 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97’dir.

• 2’den başka çift asal sayı yoktur.
• İki basamaklı en küçük asal sayı 11’dir.
• İki basamaklı en büyük asal sayı 97’dir.

Asal Çarpanlar

Bir doğal sayının çarpanlarından asal sayı olanlarına bu doğal sayının asal çarpanları denir.Asal çarpanlar, çarpan ağacı veya çarpan algoritması (bölen listesi) yöntemleri ile bulunur.

• Bir sayının asal çarpanlarını belirlemenin üç farklı yolu vardır.
• Verilen doğal sayının tüm çarpanlarını yazıp içlerinden asal olanları belirlenir.
• Verilen doğal sayı, en küçük asal sayıdan başlanarak iki sayının çarpımı şeklinde yazılır. Daha sonra bulunan sayılar asal olana kadar çarpanlara ayırmaya devam edilir. Oluşan dalların uçlarındaki sayılar verilen doğal sayının asal çarpanlarıdır. (Çarpan ağacı)
• Verilen doğal sayının yanına dikey bir çizgi çizilir. En küçük asal sayıdan başlayarak ve tam bölemediğimizde bir sonraki asal sayıya geçerek bölme işlemi yapılır. 1 elde edilince işleme son verilir. Çizginin sağında kalan sayılar verilen doğal sayının asal çarpanları olur. (Asal çarpan algoritması veya bölen listesi)

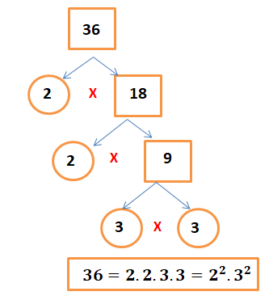
Çarpan Ağacına Örnek: