6. Sınıf Kümeler Konu Anlatımı

6. Sınıf Kümeler Konu Anlatımı, 6. Sınıf Kümeler , Kümeler Konu Anlatımı, 6. Sınıf Matematik , 6. Sınıf Matematik Konu Anlatımı, Kümeler
Kümeler
Herkes tarafından aynı şekilde anlaşılan, kişiden kişiye göre değişmeyen ve anlamlı olan varlıkların oluşturdukları topluluklara, gruplara ve birlikteliklere küme denir.
Bir topluluğun küme oluşturması için varlıkların belirli olması, anlamlı olması ve herkes tarafından aynı şekilde bilinmesi ve yorumlanması gerekir.
Örnek
“İzmir’in ilçeleri” ifadesi küme oluşturur. Çünkü herkes aynı cevabı verir.
“Ayın bazı günleri” ifadesi küme oluşturmaz. Çünkü herkesin cevabı farklı olur
Kümelerde Temel Kavramlar
• Kümeyi oluşturan her nesneye o kümenin elemanı denir.
• Elemanıdır sembolü ∈ ile gösterilir.
• Elemanı değildir sembolü ∉ ile gösterilir.
• Bir A kümesinin eleman sayısı sembolle s(A) şeklinde gösterilir.
Örnek
a, K kümesinin elemanı ise ܽ∈ şeklinde gösterilir.
∆, Y kümesinin elemanı değil ise ∆ ∉ ܻ şeklinde gösterilir.
• Hiç bir elemanı olmayan kümeye boş küme denir. Boş küme { } ya da ∅ sembolleri ile gösterilir.
Örnek
A={a, b, c, d}
B={}
Kümelerin Gösterilişi
Şema Yöntemi: Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak gösterilir. Bu gösterime Venn Şeması ile gösterim denir.
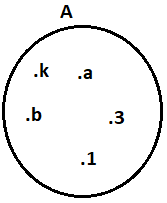
Venn Şeması gösterimi yukardaki gibidir.
Liste Yöntemi: Kümenin elemanları { } sembolü içine, her bir elemanın arasına virgül konularak yazılır.
A kümesi elemanlarını yazmak istersek şu şekilde olur; A= {k, a, 1, 3, b}.
Ortak Özellik Yöntemi: Kümeye ait elemanların tek tek yazılmak yerine ortak özelliklerinin yazılmasına ortak özellik yöntemi denir. Ortak özellik yöntemiyle kümelerin gösterimi şu şekildedir: { x | x’lerin ortak özelliği }
Öyle ki anlamına gelen “ | ” sembolü yerine “ : ” sembolü de kullanılabilir.
Örnek
X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
Y= { a, b, c, ç }
Z = { 10, 11, 12, 13 }
Kümeler ortak özellik yöntemiyle farklı şekillerde de yazılabilir. Önemli olan yazılan kümenin tam olarak (ne eksik ne fazla) kümenin elemanlarını belirtmesidir.
X = { a | a, bir rakam }
Y = { a : a, Alfabemizin ilk dört harfinden biri }
Z = { a : 9 <a < 14 , a bir doğal sayı }
Kümelerde Birleşim ve Kesişim
Birleşim İşlemi
A ve B herhangi iki küme olsun. A ve B kümelerinin tüm elemanlarının oluşturduğu kümeye A ve B kümelerinin “birleşim kümesi” denir. A ve B kümelerinin birleşim kümesi “A ∪ B” ile gösterilir, “A birleşim B” şeklinde okunur.
Kısaca; A ∪ B = {x | x ∈ A veya x ∈ B} dir.
Örnek
A={a,b,c} ve B={a,2,c} kümelerini Venn şemasında gösterelim.
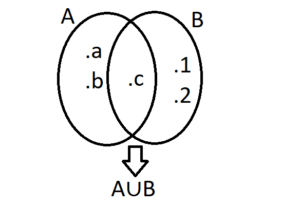
A ∪ B = { 1, 2, a,b,c }
Kesişim İşlemi
A ve B gibi iki kümenin ortak elemanlarından oluşan kümeye A ile B’nin kesişim kümesi denir ve A ∩ B biçiminde gösterilir.
A ve B kümelerinin kesişimi ortak özellik yöntemi ile A ∩ B = { x | x ∈ A ve x ∈ B } şeklinde ifade edilir.
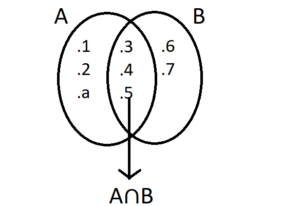
A ∩ B = { 3, 4, 5 }
Örnek
Aşağıda verilen şemanın kesişim ve birleşimlerini gösterelim.
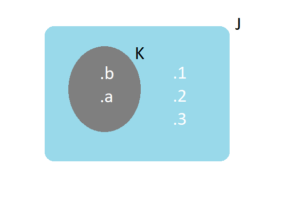
J ∩ K={a,b}
J ∪ K={a,b,1,2,3}
Biri diğerinin alt kümesi olan iki kümenin kesişimi kapsanan kümeye, birleşimi kapsayan kümeye eşittir.
s(K ∩ J) = s(M) = 2
s(K ∪ J) = s(S) =5






