7. Sınıf Çokgenler Konu Anlatımı
Çokgen, düzlemde herhangi üçü doğrusal olmayan n tane noktayı ikişer ikişer birleştiren doğru parçalarının oluşturduğu kapalı şekillerdir. 7. Sınıf Çokgenler Konu Anlatımı, 7. Sınıf Çokgenler , Çokgenler Konu Anlatımı, 7. Sınıf Matematik , 7. Sınıf Matematik Konu Anlatımı, Çokgenler
Çokgenler
- Çokgenlerin Köşegenleri, İç ve Dış Açıları
- Düzgün Çokgenler
- Dörtgenler
- Eşkenar Dörtgenin ve Yamuğun Alanı
- Alan ile İlgili Problemler
Çokgenlerin Köşegenleri, İç ve Dış Açıları
Düzlemde herhangi üçü doğrusal olmayan üç ya da daha fazla noktanın ikişer ikişer birleştirilmesiyle beraber oluşan kapalı geometrik şekillere çokgen denilmektedir.
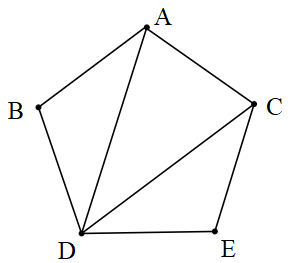
Şekildeki ABCDE çokgeninde A, B, C, D ve E noktalarına çokgenin köşeleri, [AB], [BC], [CD], [DE] ve [EA] doğru parçalarına çokgenin kenarları denir. Çokgenin içine çizilen [DA] ve [DC] doğru parçalarına çokgenin köşegenleri denir.
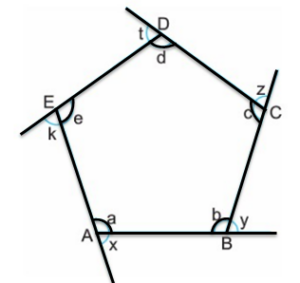
Çokgenler kenar sayısına göre isimlendirilir. Üç kenarlı ise Üçgen, dört kenarlı ise dörtgen isimini alır. ABCDE çokgeni beş kenarlı olduğundan beşgendir. Beşgenin 5 tane iç açısı, 5 tane de dış açısı vardır.
Kenar sayısı n olan bir çokgenin iç açılarının ölçüleri toplamı (n – 2). 180º formülüyle bulunur.
Örnek:
5 kenarlı bir çokgenin iç açılar toplamı (5 – 2).180° = 540°
6 kenaı1ı bir çokgenin iç açılar toplamı (6 – 2).180° = 720° ve
7 kenarlı bir çokgenin iç açılar toplamı (7 – 2).180° = 900° dir.
Dış açılar toplamı ise 3600 dir. Dış açılar toplamı kenar sayısına bağlı değildir.
Düzgün Çokgen
Tüm kenarları ve tüm iç açıları eş olan dış bükey çokgene düzgün çokgen denir.
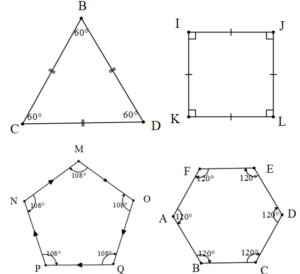
n kenarlı bir çokgende;
bir dış açısı ölçüsü: 
,
bir iç açısı:
veya 
formülleri ile bulunur.
Düzgün Çokgenler
Düzgün Çokgenin Bir Dış Açısı
n kenarlı bir düzgün çokgenin bir dış açısı ölçüsü:
Örnek
Düzgün ongen bir dış açısının ölçüsü kaç derecedir bulalım?
360 / 10 = 36°
Örnek
Bir dış açısının ölçüsü 30 derece olan düzgün çokgen kaç kenarlıdır bulalım.
360/ n = 30
30n = 360
n = 12
Düzgün Çokgenin Bir İç Açısı
n kenarlı bir düzgün çokgenin bir iç açısı:veya formülleri ile bulunur.
Örnek
12 kenarlı bir çokgenin iç açısını bulalım.
(12-2) . 180 /12= 10 . 180 /12 = 150º
Örnek
25 kenarlı bir çokgenin iç açısını bulalım.
(25 – 2) . 180 / 25 = 23. 180 / 25 = 165,6º
Dörtgenler
Herhangi üçü doğrusal olmayan A, B, C, D noktalarını birleştiren [AB], [BC], [CD] ve [DA] doğru parçalarının birleşiminden oluşan kapalı şekle dörtgen denir.
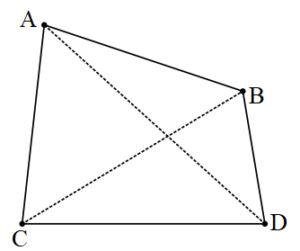
Şekildeki A, B, C, D noktalarına dörtgenin köşeleri, [AB], [BD], [DC] ve [AC] doğru parçalarına dörtgenin kenarları denir. Birer köşesi ortak olan kenarlara komşu kenarlar, ortak köşesi olmayan kenarlara ise karşı kenarlar denir. [AD] ve [BC] doğru parçalarına dörtgenin köşegenleri denir.
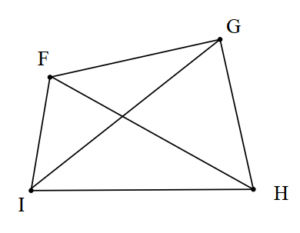FGHI dışbükey dörtgen
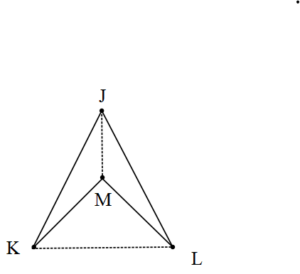JKLM içbükey dörtgen
Dörtgende Açı Özellikleri
1. Dörtgenlerin iç açıları toplamı 360º’dir.
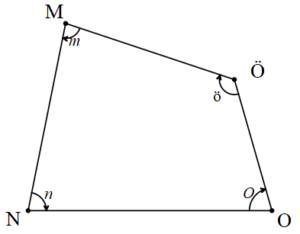
k+m+o+ö=360
2. Dörtgenlerin dış açıları toplamı 360º’dir.
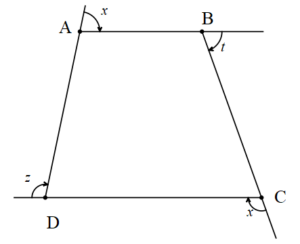
3. a, b, c, d iç açılar ve x, y, z, t dış açılar olmak üzere,
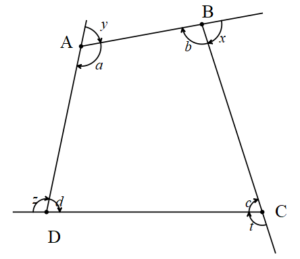
a + c = y + t
b + d = x + z dir.
4. ABCD dörtgeninde [AE] ve [BE]açıortay ise
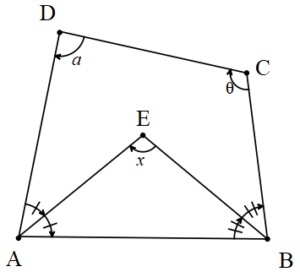
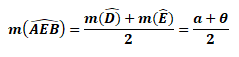
Dörtgenlerde Uzunluk
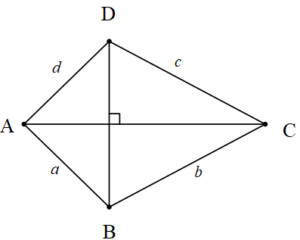
ABCD dörtgeninde [AC] ve[DB] ise
a2+c2=d2+b2
Eşkenar Dörtgenin ve Yamuğun Alanı
Eşkenar Dörtgenin Alanı
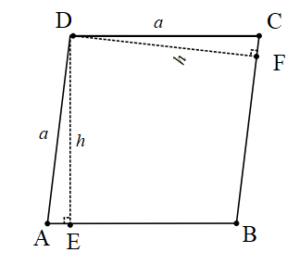
ABCD eşkenar dörtgen
|AD| = |DC|=a br
|DE| = |DF|=h br
Alan(ABCD)= a.h
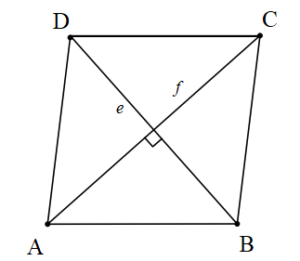
ABCD bir eşkenar dörtgen
[AC] ve[DB] köşegen
[AC] ⊥ [DB]
|BD|=e
|AC|=f
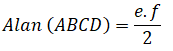
Yamuk ve Özellikleri – Yamuğun Alanı
Karşılıklı iki kenarı paralel olan dörtgene yamuk denir.
1. [AB]//[DC] olduğundan ABCD bir yamuktur.
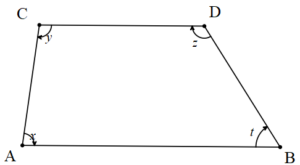
2. Yamukta paralelkenarlar arasında kalan iki açı bütünlerdir.
x+y=180º’dir ve z+t=180º
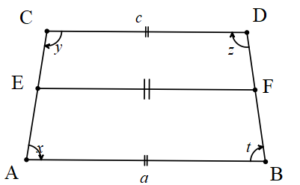
[AB]//[DC]//[EF]
[EF] orta taban
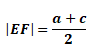
3. [AB]//[DC]//[EF] , [EF] orta taban
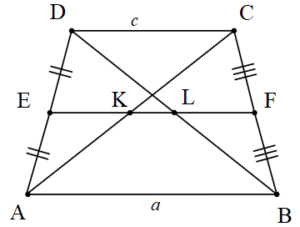
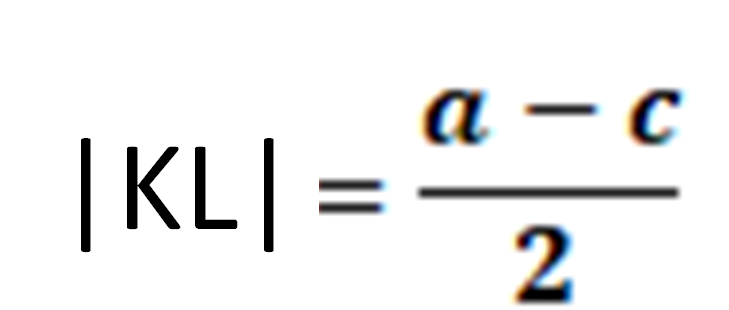
4. [AB]//[DC]//[EF]
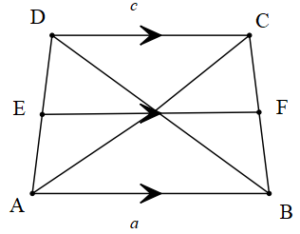
İkizkenar Yamuk ve Özellikleri
Yan kenar uzunlukları birbirine eşit olan yamuğa ikizkenar yamuk denir.
ABCD ikizkenar yamuk
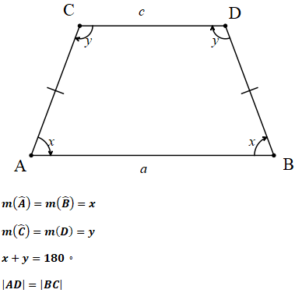
İkizkenar yamuğun köşegen uzunlukları birbirine eşittir.
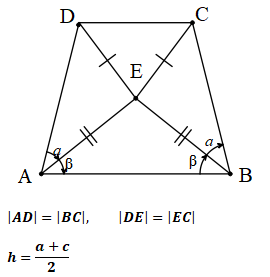
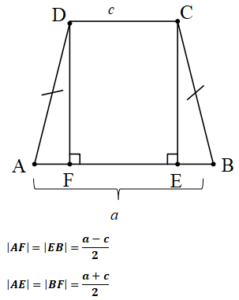
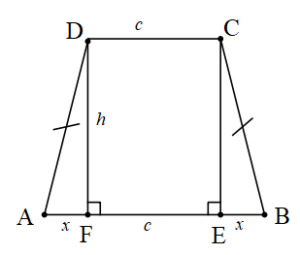
A(ABCD)=h.(c+x)
Dik Yamuk ve Özellikleri
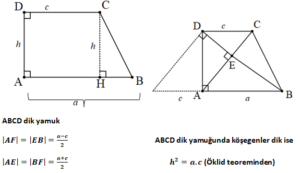
Yamuğun Alanı
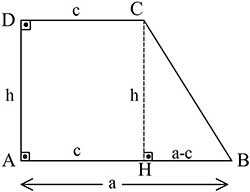
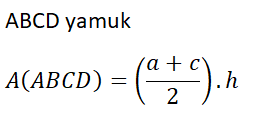
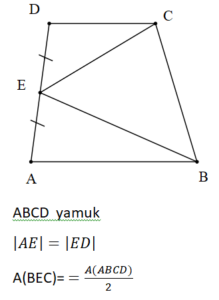
Alan ile İlgili Problemler
Örnek-1
Aşağıda taban kenar uzunlukları ve yüksekliği verilen yamuğun alanını bulunuz.
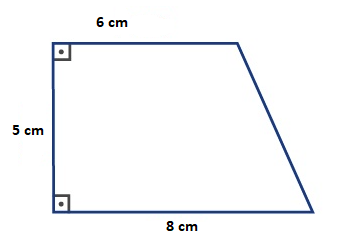
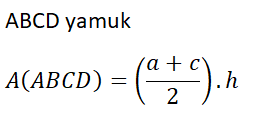
6 + 8 . 5 / 2 = 14. 5 /2 = 70 /2 = 35 cm2
Örnek-2
Aşağıda taban kenar uzunlukları ve yüksekliği verilen yamuğun alanını bulunuz.
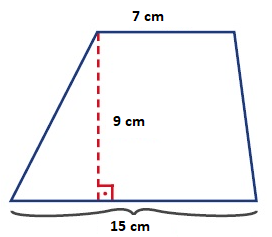
15 + 7 .9 / 2 = 22. 9 / 2 = 198/ 2 = 99 cm2
Örnek-3
Aşağıda köşegen uzunlukları verilen eşkenar dörtgenin alanını bulunuz.
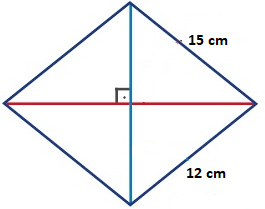
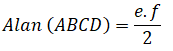
15. 12 / 2 = 180 / 2 = 90 cm2
