7. Sınıf Oran ve Orantı Konu Anlatımı

Orantı matematikte iki değişken arasındaki ilişkidir. İki değişken arasında sabit bir çarpan olması haline doğru orantı veya kısaca orantı denilir.7. Sınıf Oran ve Orantı Konu Anlatımı, 7. Sınıf Oran ve Orantı , Oran ve Orantı Konu Anlatımı, 7. Sınıf Matematik, 7. Sınıf Matematik Konu Anlatımı, Oran ve Orantı
Oran ve Orantı
- Oranda Çokluklardan Birinin 1 Olması Durumunda Diğerinin Alacağı Değer
- Birbirine Oranı Verilen İki Çokluktan Biri Verildiğinde Diğerini Bulma
- Orantı
- Doğru Orantılı İki Çokluk Arasındaki İlişki
- Doğru Orantılı İki Çokluğa Ait Orantı Sabiti
- Ters Orantılı İki Çokluk Arasındaki İlişki ve Orantı Sabiti
- Doğru ve Ters Orantıyla İlgili Problemler
Oranda Çokluklardan Birinin 1 Olması Durumunda Diğerinin Alacağı Değer
Bir oranda çokluklardan biri 1 olduğunda diğerinin alacağı değeri bulduğumuzda, aslında değeri 1 (bir) olan çokluğun birim değerini bulmuş oluruz.
Örnek
Bir çocuk bakkaldan aldığı 15 kilogram şekere 30 lira ödemiştir. Buna göre aşağıda istenenleri beraber bulalım.
a) Bu çocuk 1 kilogram şeker için kaç lira ödemiştir?
b) Bu çocuk 1 lira ile kaç kilogram şeker almıştır?
a) 1 kg şeker için kaç lira ödediğini bulurken, ödediği toplam parayı aldığı toplam şeker miktarına bölmemiz gerekir.
olarak bulunur.
![]()
Çocuk bakkaldan satın aldığı 1 kg şekere 0,5 lira para ödemiştir.
b) 1 lira ile kaş kg şeker aldığını bulurken, toplam şeker miktarını ödediği toplam paraya bölmemiz gerekir.
![]()
Birbirine Oranı Verilen İki Çokluktan Biri Verildiğinde Diğerini Bulma
Birbirine oranı verilen iki çokluktan biri verildiğinde diğerini bulmak için verilen orana göre bir eşitlik oluşturulur. Elde edilen eşitlikte oranların birbirinin kaç katı olduğu bulunarak verilmeyen değer bulunur.
Örnek
Bir sınıftaki kız öğrencilerin sayısı erkek öğrencilerin sayısına oranı ![]() tir. Sınıfta 20 kız öğrenci olduğuna göre erkek öğrenci sayı kaçtır?
tir. Sınıfta 20 kız öğrenci olduğuna göre erkek öğrenci sayı kaçtır?

Orantı
En az iki oranın birbirine eşit olması durumuna orantı denir.
![]()
![]() şeklinde gösterilir.
şeklinde gösterilir.
Doğru Orantılı İki Çokluk Arasındaki İlişki
İki çokluktan biri artarken diğeri de aynı oranda artıyorsa ya da biri azalırken diğeri de aynı oranda azalıyorsa bu çokluklar doğru orantılıdır.
Örnek
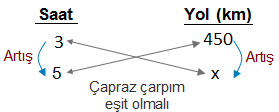
3 saatte 450 km yol giden bir araç 5 saatte kaç km yol gider?
3 saatte 450 km yol giden araç 5 saatte daha fazla yol alır. Bu durumda hem saatte hem de yolda artış vardır. Bu nedenle orantımız doğru orantıdır.
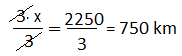
Doğru Orantılı İki Çokluğa Ait Orantı Sabiti
Doğru orantılı çoklukların bölümü sabit bir sayıdır. Bu sayıya orantı sabiti denir.
Örnek
Bir otomobil sabit hızla 1 saatte 70 km yol gidebiliyor.
otomobil sabit hızla gittiğinde 2 saatte 140 3 saatte 210 km yol alır.
![]()
Yolun zamana oranı 70 dir.
Ters Orantılı İki Çokluk Arasındaki İlişki ve Orantı Sabiti
Orantıda bulunan çokluklardan biri artarken, diğeri azalıyor veya biri azalırken, diğeri artıyor ise bu orantıya Ters Orantı denir. Ters orantıda karşılıklı çarpımlar eşitlenir.
Örnek
Ortalama 100 km/s hızla gittiğimizde 6 saatte tamamladığımız bir yolu, 120 km/s hızla gidersek kaç saatte tamamlarız?
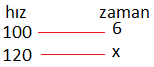
100 . 6 = 120. x
600 = 120 x
600 /120 = 120.x / 120
x= 5 saatte tamamlanır.
Ters orantılı çoklukların çarpımı sabit bir sayıdır.
Örnek
Bir işi bir işçi 24 saatte bitiriyor. 2 işçi 12 saatte, 4 işçi 6 saatte bitiriyor.
1.24 = 2. 12 = 4. 6 = 24
Doğru ve Ters Orantıyla İlgili Problemler
1. Günlük uyuma süresi sabit olan Ayşe, 9 günde 63 saat uyursa bir haftada kaç saat uyur?
Çözüm
1 hafta 7 gün.
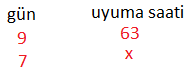
Sorumuzu çözerken doğru orantı ve orantı sabitini kullanabiliriz.
1. yol
63: 9 = 7 günlük uyuma süresi.
7. 7 = 49 saat
2. Yol
9 . x = 7 . 63
9x = 441
x = 49 saat
2. 14 kg zeytinden 5 kg zeytinyağı elde edilebiliyor. Buna göre 35 kg zeytinden kaç kg zeytinyağı elde edilebilir?
Çözüm
| zeytin kg | zeytin yağı kg |
| 14 | 5 |
| 35 | x |
14. x = 35. 5
14 x = 175
x= 12,5 kg zeytin yağı elde edilir.
3. Birbirini döndüren büyük çark 15 küçük çark 8 dişlidir. Büyük çark 72 tur dönüğünde küçük çark kaç turda döner?
Çözüm
| dişli sayısı | tur sayısı |
| 15 | 72 |
| 8 | x |
Ters orantı kullanarak problemimizi çözelim.
15 . 72 = 8 . x
1080 = 15x
x = 135 turda döner.
4. 6 işçi bir duvarı 4 günde boyayabiliyor. Aynı duvarı 3 işçi kaç günde boyar?
Çözüm
| işçi | gün |
| 6 | 4 |
| 3 | x |
Ters orantı kullanarak problemimizi çözelim.
6 . 4 = 3. x
24 = 3x
x = 8 günde boyar.
5. Bir havuzu 6 özdeş musluk 20 saatte doldurabildiğine göre 5 özdeş musluk aynı havuzu kaç saatte doldurur?
Çözüm
| musluk | saat |
| 6 | 20 |
| 8 | x |
Ters orantı kullanarak problemimizi çözelim.
6 . 20 = 8. x
120 = 8x
x= 15 saatte doldurur.
6. Limonata yapımında kullanılan şeker, limon ve su miktarları sırasıyla 2, 3 ve 4 sayılarıyla orantılıdır. 720 gr limonata yapıldığına göre aşağıdakilerden hangisi bu malzemelerden birine ait miktar değildir?
Çözüm
Şeker = 2k
Limon = 3k
Su = 4k
Limonata = 2k + 3k + 4k
720 = 9k
80 = k
Şeker = 2 . k = 2 . 80 = 160 gr
Limon = 3 . k = 3 . 80 = 240 gr
Su = 4 . k = 4 . 80 = 320 gr
7. Sınıf Matematik Konuları için tıklayınız.






