Diziler Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Diziler konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Diziler
- Dizinin Tanımı Özellikleri
- Aritmetik Dizi ve Özellikleri
- Geometrik Dizi ve Özellikleri
- Fibonacci Dizisi
Dizinin Tanımı Özellikleri
Pozitif doğal sayılar kümesinden gerçek sayılar kümesine tanımlanan her fonksiyona gerçek sayı dizisi veya dizi denir.

Genel Terimi an olan dizi;

Dizinin Özellikleri

Sabit Dizi: Bütün terimleri birbirine eşit olan dizilerdir.


Aritmetik Dizi ve Özellikleri
Ardışık terimleri arasındaki fark eşit olan diziye aritmetik dizi denir. Her n Є Z+ ve d Є R için ![]() eşitliğini sağlayan dizilerdir. Burada d, aritmetik dizinin ortak farkıdır.
eşitliğini sağlayan dizilerdir. Burada d, aritmetik dizinin ortak farkıdır.

Örnek:
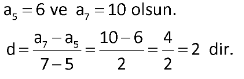
Aritmetik Dizinin Özellikleri

Geometrik Dizi ve Özellikleri
Ardışık terimleri arasındaki oran sabit olan dizilere geometrik dizi denir. Bu sabit oran, ortak çarpandır (r).
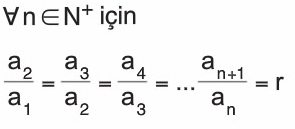
Geometrik Dizilerde Genel Terim
an+1 = an . r
a2 = a1 . r
a3 = a2 . r = a1 . r2
a4 = a3 . r = a1 . r3
….
an = an-1 . r = a1 . rn-1
Sonuç olarak geometrik dizinin genel terimi an = a1 . rn-1 bulunur.
Geometrik Dizinin Özellikleri
1. İlk terim a1, ortak çarpanı r olan geometrik dizinin genel terimi
![]()
2. Bir geometrik dizide bir terimin karesi kendisinden eşit uzaklıkta bulunan iki terimin çarpımına eşittir.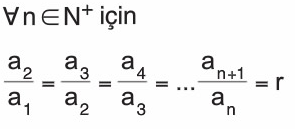
3. Bir geometrik dizide ilk n terimin toplamı Sn ise;
![]()
2. Ortak çarpanı bulmak için ;
Ardışık iki terim verildiğinde:
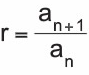
Herhangi iki terim verildiğinde:
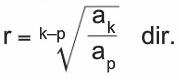
a,…., b sayıları arasına n terim yerleştirip bir geometrik dizi oluşturmak için;
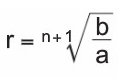
Fibonacci Dizisi
Her terimi kendisinden önce gelen iki terimin toplamı şeklinde yazılabilen dizilere fibonacci dizisi denir.
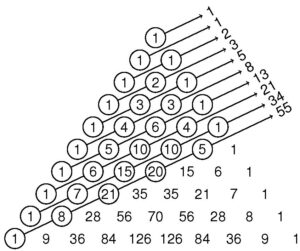
Fibonacci dizisinin terimleri 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Fibonacci dizisinin en önemli özelliklerinden biri , bu dizinin ardışık terimleri oranının, terimler büyüdükçe altın orana ![]() yaklaşmasıdır.
yaklaşmasıdır.
Fibonacci dizisinin genel terimi Fn ile gösterilirse, bu dizinin indirgenme bağıntısı F1=F2=1 olmak üzere,
Fn+2=Fn+1+Fn olur.
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.







Hepinizden Allah razı olsun Allah tuttuğunuzu altın etsin çok güzel olmuş
Aritmatik diziler özet ve kurallar bakımından gayet başarılı bir biçimde anlatılmış. Ancak geometrik diziler daha iyi anlatılabilirdi. Yine de emeğinize sağlık güzel, faydalı bir içerik olmuş.