Limit Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Limit konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Limit
- Soldan Yaklaşma, Sağdan Yaklaşma
- Limit Kavramı
- Limitin Özellikleri
- Parçalı Fonksiyonun Limiti
- Mutlak Değer Fonksiyonunun Limiti
- 0/0 Belirsizliği
Soldan Yaklaşma, Sağdan Yaklaşma
x değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir ve x → a– biçiminde gösterilir.
x değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve x →a+ biçiminde gösterilir.
Limit Kavramı
Bir f(x) fonksiyonunda x değişkenine bir a değerine sınırsız yaklaşan değerler verildiğinde fonksiyondaki f(x) değerleri de bir L değerine sınırsız yaklaşıyorsa; bu L değerine f(x) fonksiyonunun a değeri için limiti denir.
Önemli
![]()

şeklinde gösterilir.
![]()

şeklinde gösterilir.
![]()
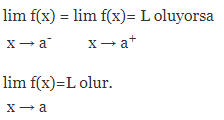
şeklinde gösterilir.
![]()
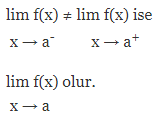
şeklinde gösterilir.
lim f(x) ifadesinin alabileceği tek bir x→ a değer vardır.
f(x) fonksiyonu x=a için tanımsız olsa olsa bile lim f(x) bulunabilir.
x→a
Çünkü lim f(x) demek f(a) demek değil x→a ” x,a’ya yaklaşırken f(x)’in yaklaştığı değer demektir.
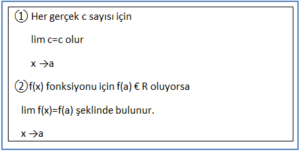
Limitin Özellikleri




Parçalı Fonksiyonun Limiti
Belirli reel sayı aralıklarına göre tanımlamaları yapılmış bir parçalı fonksiyonda bu aralıkların sınır değerleri olan gerçek sayılar fonksiyonun kritik noktalarıdır.
Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “gerçek sayının bulunduğu aralık için tanımlanan fonksiyonun, bu gerçek sayı için limiti bulunur.”
![]()

Kritik noktalar için limit incelemesi yapılırken, kritik nokta için sağdan ve soldan limit incelenir. “Kritik nokta için sağdan limit ile soldan limit aynı L değerine eşit oluyorsa, kritik nokta için fonksiyonun limiti L olur.”

![]() Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.”
Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.”
Mutlak Değer Fonksiyonunun Limiti
Bir mutlak değer fonksiyonunda bulunan mutlak değer içindeki ifadeyi sıfırlayan gerçek sayı, bu fonksiyonun kritik noktasıdır.
Kritik noktalar dışındaki herhangi bir gerçek sayı için fonksiyonun limitini bulmak istersek; “Bu gerçek sayıyı fonksiyonda doğrudan yerine yazıp sonucu buluruz.”
Örnek:
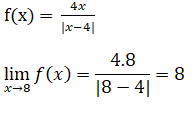
Kritik noktalar için limit incelemesi yapılırken, kritik nokta için sağdan ve soldan limit incelenir. “Kritik nokta için sağdan limit ile soldan limit aynı L değerine eşit oluyorsa, kritik nokta için fonksiyonun limiti L olur.”

![]() Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.”
Kritik nokta için sağdan ve soldan limit incelemesi sonucunda; “sağdan limit ile soldan limit farklı değerler çıkıyorsa bu kritik nokta için fonksiyonun limiti yoktur.”
0/0 Belirsizliği

![]() Pay veya paydada köklü ifadelerin bulunması durumunda sadeleştirme işleminden önce “pay ve paydayı eşlenikle çarpmak” gerekebilir.
Pay veya paydada köklü ifadelerin bulunması durumunda sadeleştirme işleminden önce “pay ve paydayı eşlenikle çarpmak” gerekebilir.
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.







hic anlayamadim malesef cok uzgunum galiba intihar edecegim!
sacmalam dostum
proje ödevim için çok işe yaradı teşekkürler