Çemberin Analitik İncelemesi Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Çemberin Analitik İncelemesi konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Çemberin Analitik İncelemesi
Çember Denklemi
Düzlemde sabit bir noktadan eşit uzaklıkta bulunan noktaların kümesine çember denir. Sabit noktaya çemberin merkezi, çember üzerindeki herhangi bir noktanın çemberin merkezine olan uzaklığına ise çemberin yarıçapı denir.

Merkezi ve Yarıçapı Verilen Çemberin Denklemi

ÖRNEK
Merkezi M(2, 3) ve yarıçapı r=4 birim olan çemberin standart denklemini bulunuz.
ÇÖZÜM

ÖRNEK
A(2, -1 ) ve B(-4, -5) olmak üzere [AB] çaplı çemberin standart denklemini bulunuz.
ÇÖZÜM
Çemberin merkezi ile çember üzerindeki herhangi bir nokta arasındaki uzaklık, çemberin yarıçapını verir.

Bazı Özel Çemberlerin Denklemleri
1. Merkezi Orijinde Olan Çemberin Denklemi
Merkezi orijinde ve yarıçapı r birim olan çemberin standart denklemi;

2. Merkezi x Ekseni Üzerinde Olan Çemberin Denklemi
Merkezi x ekseni üzerinde bulunan bir çemberde merkezin koordinatları M(a, 0) olacaktır. Çemberin yarıçapı r birim ise bu çemberin standart denklemi;

3. Merkezi y Ekseni Üzerinde Olan Çemberin Denklemi
Merkezi y ekseni üzerinde bulunan bir çemberde merkezin koordinatları M(0, b) olacaktır. Çemberin yarıçapı r birim ise bu çemberin standart denklemi;
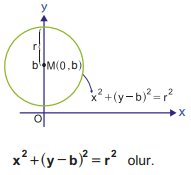
4. y Eksenine Teğet Olan Çemberin Denklemi
Merkezi M(a,b) ve yarıçapı r birim olan bir çember, y eksenine teğet ise r = a olur. Bu durumda çemberin standart denklemi;

5. x Eksenine Teğet Olan Çemberin Denklemi
Merkezi M(a,b) ve yarıçapı r birim olan bir çember, x eksenine teğet ise r = b olur. Bu durumda çemberin
standart denklemi;
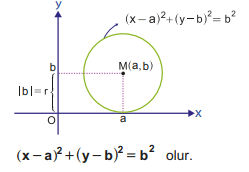
6. Her İki Eksene de Teğet Olan Çemberin Denklemi
Çember her iki eksene de teğet ise r =|a| = |b| olur. Bu durumda eksenlere teğet olan çemberlerin merkezleri y = x veya y =- x doğruları üzerinde olacaktır. Eğer çemberin merkezi


ÖRNEK
Merkezi M(-3,2) olan çember A noktasında x eksenine teğettir. Bu çemberin standart denklemini bulunuz.
ÇÖZÜM
|MA| = r olup r=2 birim bulunur. Merkezi M(-3,2), ve yarıçapı r=2 birim olan çemberin standart denklemi
![]()

Çemberin Genel Denklemi
Analitik düzlemde M( a, b) merkezli ve r yarıçaplı çember üzerinde bir P(x, y) noktası alınırsa M(a, b) ile P(x, y) noktaları arasındaki uzaklık

ÖRNEK
Merkezi M(2, 3)ve yarıçapı r=4 birim olan çemberin standart denklemini bulunuz.
ÇÖZÜM

Bazı Özel Çemberlerin Denklemleri
1. Merkezi Orijinde Olan Çemberin Denklemi
Merkezi orijinde ve yarıçapı r birim olan çemberin standart denklemi

2. Merkezi x Ekseni Üzerinde Olan Çemberin Denklemi
Merkezi x ekseni üzerinde bulunan bir çemberde merkezin koordinatları M(a, 0) olacaktır. Çemberin yarıçapı r birim ise bu çemberin standart denklemi

3. Merkezi y Ekseni Üzerinde Olan Çemberin Denklemi
Merkezi y ekseni üzerinde bulunan bir çemberde merkezin koordinatları M(0, b) olacaktır. Çemberin yarıçapı r birim ise bu çemberin standart denklemi

4. y Eksenine Teğet Olan Çemberin Denklemi
Merkezi M(a,b) ve yarıçapı r birim olan bir çember, y eksenine teğet ise r = a olur. Bu durumda çemberin
standart denklemi

5. x Eksenine Teğet Olan Çemberin Denklemi
Merkezi M(a,b) ve yarıçapı r birim olan bir çember, x eksenine teğet ise r = b olur. Bu durumda çemberin
standart denklemi

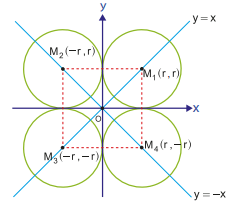
6. Her İki Eksene de Teğet Olan Çemberin Denklemi
Çember her iki eksene de teğet ise r =|a|=|b| olur. Bu durumda eksenlere teğet olan çemberlerin merkezleri y=x veya y=-x doğruları üzerinde olacaktır. Eğer çemberin merkezi

ÖRNEK
Merkezi M( -3, 2) olan çember A noktasında x eksenine teğettir. Bu çemberin standart denklemini bulunuz.
ÇÖZÜM

Çemberin Genel Denklemi
Merkezi M(a, b) ve yarıçapı r birim olan çemberin standart denklemi
![]()
şeklindedir. Bu denklem düzenlenerek

denklemi elde edilir. Bu denkleme çemberin genel denklemi denir.

Çemberin yarıçapı


ÖRNEK
![]()
ÇÖZÜM

Merkezi M(a, b) ve yarıçapı r birim olan çemberin standart denklemi olan

çemberin genel denklemine dikkat edilirse denklemde xy li terimin bulunmadığı görülür.
Ayrıca bu denklemde eşitliğin her iki tarafı sabit bir k sayısı ile çarpılırsa yukarıdaki ifadeye özdeş
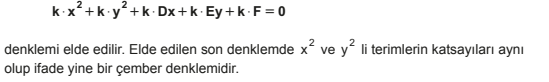

ÖRNEK
![]() denkleminin bir çember belirtip belirtmeyeceğini, çember belirtiyorsa merkezini ve yarıçapını bulunuz.
denkleminin bir çember belirtip belirtmeyeceğini, çember belirtiyorsa merkezini ve yarıçapını bulunuz.
ÇÖZÜM
![]() i terimlerin katsayıları farklı olduğundan bu denklem bir çember belirtmez. Denklem bir çember belirtmediği için merkezinden ve yarıçapından söz edilemez.
i terimlerin katsayıları farklı olduğundan bu denklem bir çember belirtmez. Denklem bir çember belirtmediği için merkezinden ve yarıçapından söz edilemez.
Denklemleri Verilen Doğru ile Çemberin Birbirine Göre Durumları


ÖRNEK
![]()
ÇÖZÜM

12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.







kısa ve güzel bir anlatım olmuş
teşekkürler