Matematik ayt konu anlatımı, Matematik tyt konu anlatımı , Matematik yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Fonksiyonlarla İşlemler ve Uygulamalar Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Fonksiyonlarla İşlemler ve Uygulamalar

• Fonksiyonlarla İşlemler
• Fonksiyonlarda Uygulamalar

Fonksiyonlarla İşlemler

Fonksiyonlarda Uygulamalar

İkinci Dereceden Fonksiyonların Grafikleri (Parabol)

a, b, c, ∈ R ve a ≠ 0 olmak üzere;
y = ax² + bx + c

biçiminde tanımlanan fonksiyonlara, ikinci dereceden fonksiyonlar denir. x değişkeni R (gerçek sayılar kümesi) den seçilirse, R den R ye bir ikinci derece fonksiyonu elde edilir. Fonksiyonun analitik düzlemdeki grafiği olan eğriye parabol denir.

parabolü analitik düzlemde gösterebilmek (çizebilmek) için yapılması gereken işlemleri aşağıdaki
gibi sıralayabiliriz.
* Tepe noktasının koordinatları bulunur.
* Grafiğin varsa, koordinat eksenlerini kestiği noktalar bulunur.
* Değişim tablosu düzenlenir.
* Değişim tablosundan yararlanarak, belirlenen noktalar analitik düzlemde işaretlenir ve grafik çizilir.

Örnek

y = 2x² + 8 parabolünün varsa, eksenleri kestiği noktaları bulalım.

x = 0 için, y = 2.0² + 8 = 8 olduğundan, y eksenini kestiği nokta (0. 8) dir.
y = 0 için, 0 = 2x² + 8 ⇒ 2x² = -8 ⇒ x² = – 4 gerçek kök yoktur.
O halde, parabolün x eksenini kestiği noktası yoktur.

Parabolün Tepe Noktasının Koordinatları

f(x)= ax² + bx + c parabol grafiğinde tepe noktası T(r,k) olmak üzere

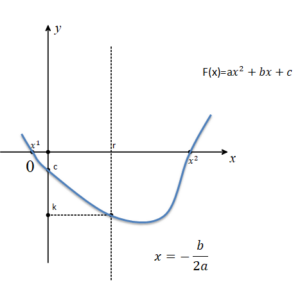
Parabolün En Büyük ve En Küçük Değeri

f(x) = ax² + bx + c parabolünde

a > 0 ise parabolün alabileceği en küçük değer parabolün tepe noktasının ordinatıdır.

a < 0 ise parabolün alabileceği en büyük değer tepe noktasının ordinatıdır.

Bu durum parabolün herhangi bir aralıktaki parçası için geçerli değildir.
[a, b] aralığındaki parabolün maksimum-minimum değeri sorulursa tepe noktası T(r, k) olmak üzere f(r), f(a) ve f(b) ye bakılır.

Tepe Noktası ve Bir Noktası Bilinen Parabol Denklemi

T(r, k) parabolün tepe noktası ve A(x₀, y₀) parabol üzerinde bir nokta ise parabolün denklemini bulmak için

y = a.(x – r)² + k

yazıldıktan sonra a değerini bulmak için verilen nokta yerleştirilir.

x Eksenin Kestiği Noktalar ve Üzerindeki Başka Bir Noktası Bilinen Parabolün Denklemi

f(x) parabolünün x eksenini kestiği noktalar A(x₁, 0) ve B(x₂, 0) ise parabolün denklemi
f(x) = a. (x – x₁) . (x – x₂) biçiminde yazılır. Bilinmeyen a değerini bulmak için parabolün üzerindeki nokta denklemde yazılır.

Üç Noktası Bilinen Parabol Denklemi

A(x₀, y₀) , B(x₁, y₁) ve C(x₂, y₂) noktaları parabolün üzerinde ise üçü de parabolün denklemini sağlar. Bu noktalar parabolün genel denklemi olan

y=f(x) =ax² + bx + c de yerleştirilirse üç bilinmeyenleri üç denklem çözülür a, b, c değerleri bulunur.

Bir Doğru İle Bir Parabolün Birbirlerine Göre Durumları

y = ax² + bx + c parabolü ile
y = mx + n

doğrusunun denklemleri birbirine eşitlenip oluşan denklemin diskriminantına bakılır. (Δ = b² – 4ac)

Δ > 0 ise parabol ve doğru iki noktada kesişir.
Δ = 0 ise parabol doğruya teğettir.
Δ < 0 ise parabolle doğru kesişmez.

parabolünün x eksenini kesip kesmediğini yorumlamak için x ekseni y = 0 doğrusu olduğundan

ax² + bx + c = 0 denkleminin diskriminantına bakılır.

Δ > 0 ise parabol x eksenini iki farklı noktada keser.
Δ = 0 ise parabol x eksenine teğettir.
Δ < 0 ise parabol x eksenini kesmez.

Fonksiyonların Dönüşümleri

Tek Fonksiyon

Grafiği orijine göre simetrik olan fonksiyonlar tek fonksiyondur.

Tek fonksiyonda her x ∈ R için f(-x) = -f(x) sağlanır.
Tek fonksiyonlarda x’in çift kuvvetlerinin olduğu terimlerin katsayıları sıfırdır.

Örnek:

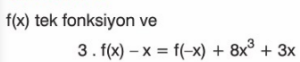
Çözüm:

Çift Fonksiyon

Grafiği y eksenine göre simetrik olan fonksiyonlara çift fonksiyon denir.

Çift fonksiyonlar her x ∈ R için f(-x) = f(x) olur.
Çift fonksiyonlarda x’in tek kuvvetlerinin olduğu terimlerin katsayıları sıfırdır.

Örnek:

Çözüm:

Fonksiyonların Dönüşümleri

♦ b € R olmak üzere f(x)+b fonksiyonunun grafiği f(x) fonksiyonun grafiğinin b birim yukarı ötelenmesi ile elde edilir.

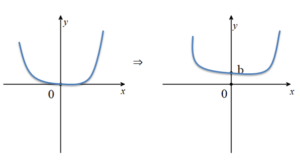
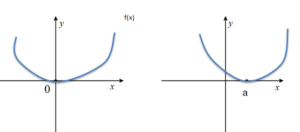
♦a € R olmak üzere f(x-a) fonksiyonunun grafiği f(x) fonksiyonunun grafiğinin x ekseninde a birim ötelenmesi ile elde edilir.

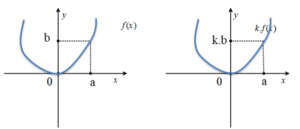
k € R olmak üzere k. f(x) fonksiyonunun grafiği f(x) fonksiyonundaki değerlerin k ile çarpılması ile elde edilir.

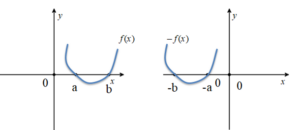
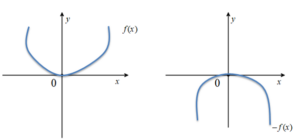
-f(x) fonksiyonunun grafiği f(x) fonksiyonunun x eksenine göre simetriği alınarak elde edilir.

f(-x) fonksiyonunun grafiği f(x) fonksiyonunun grafiğinin y eksenine göre simetriği alınarak elde edilir.