Olasılık Konu Anlatımı

Matematik ayt konu anlatımı, Matematik tyt konu anlatımı , Matematik yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Olasılık Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Olasılık

Olasılıkla İlgili Terimler
Örnek Uzay
Olasılık Hesabı
Olasılıkların Toplamı
Bağımsız Olaylar
Koşullu Olasılık

Olasılıkla İlgili Terimler

Deney: Bir olayın sonucunun ne olacağını görmek için yapılan işleme deney denir.
Çıktı: Deneyin sonucunda elde edilebilecek sonuçlara çıktı denir.
Örnek Uzay: Bir deneyde elde edilebilecek tüm çıktıların kümesine Örnek uzay denir ve E ile gösterilir.
Örnek Nokta: Ömek uzayın herhangi bir elemanına örnek nokta denir.

Örnek:

Madeni bir paranın havaya atılması deneyinde, para yere düşmeden kesin olarak yazı mı, tura mı geleceğini bilemeyiz.

Bu deneyin çıktıları yazı veya turadır. Yazıyı Y, turayı T harfi ile gösterirsek, tüm çıktıların oluşturduğu küme örnek uzay olacağı için E = {Y, T} olur. Yazı gelmesi ya da tura gelmesi ise bir olaydır.

İmkansız Olaylar: Gerçekleşmesi mümkün olmayan olaylar,

Bir zarın atılması deneyinde üst yüze gelen sayının 6 dan büyük olması gerçekleşmesi mümkün olmayan olaydır.

Kesin Olaylar: Gerçekleşmesi kesin olan olaylardır,

Sadece erkeklerin bulunduğu bir sınıftan seçilen öğrencinin erkek olma olayı kesin olaydır.

Eşit Olasılıklı Olaylar: Bir zarın havaya atılması deneyinde üst yüze birden altıya kadar olan sayıların gelmesi eşit olasılıklı olaydır.

Bir madeni para atıldığında yazı ve tura gelme olasılığı birbirine eşittir.

Daha Fazla Olasılıklı Olaylar: 10 tane kız 5 tane erkek bulunan bir sınıftan seçilen öğrencinin kız olma olasılığı daha fazladır.

Daha Az Olasılıklı Olaylar : 40 tane kırmızı 2 tane mavi top bulunan bir torbadan seçilen topun mavi olma olasılığı daha azdır.

Örnek Uzay

Bir deney sonucunda ortaya çıkan tüm durumların kümesine örnek uzay denir.

Örnek:

2 madeni para atıldığında ortaya çıkan durumlar, (Y,T),(T,Y),(Y,Y),(T,T) olmak üzere 4 tanedir.

Örnek uzay bulunurken;

n tane madeni para atıldığında örnek uzayın eleman sayısı dir. n tane zar atıldığında da örnek uzayın eleman sayısı dir.

Olasılık Hesabı

Bir A olayının olma olasılığı P(A) ile gösterilir ve bu olasılık

ile hesap edilir.

P(A) bir A olayının olma olasılığı ise P(A’), A olayının olmama olasılığıdır ve P(A)+P(A’)=1 dir.

Bir A olayının olasılığı daima 0 ≤ P(A) ≤ 1 dir.

Örnek:

Bir A olayının olma olasılığı, B olayının olma olasılığının 3 atı, C olayının olma olasılığının yarısıdır.

Buna göre B olayının olmama olasılığı kaçtır?

Çözüm:

A,B ve C olaylarının olasılıkları toplamı daima 1 dir.

3x+x+6x=1

B olayının olma olasılığı (1-P(B))’ dir.

Örnek:

Bir çift zar bitlikte atılıyor.

Zarların üst yüzüne gelen sayılar toplamının 8 den büyük olma olasılığı nedir?

Çözüm:

Bütün durum

İstenilen durum:

(6,3),(3,6),(4,5),(5,4) → toplamları 9 olan(4 tane)
(6,4),(4,6),(5,5)→ toplamları 10 olan(3 tane)
(6,5),(5,6)→ toplamları 11 olan(2 tane)
(6,6) → toplamları 12 olan (1 tane)

Olasılıkların Toplanması

Olasılıkları hesaplanacak olaylar arasona soruda “veya” bağlacı getirilirse olasılıklar toplanır.

Yani, A veya B’nin olasılığı

P(A∪B)=P(A)+P(B)-P(A∩B)

Örnek:

Bir torbada 5 tane mavi,3 tane yeşil ve 2 tane kırmızı top bulunmaktadır.

Torbadan rastgele çekilen bir topun mavi veya kırmızı gelme olasılığı kaçtır?

Çözüm:

M:Mavi K:Kırmızı

Mavi veya kırmızı top gelme olasılığı

P(M∪K)=P(M)+PK)-P(M∩K) (Altı çizili kısım ayrıl olay)

Bağımsız Olaylar

Birbirinin olasılığını etkilemeyen(örneklem uzayları farklı) iki olay soruda “ve” bağlayıcı ile birbirine bağlanır. Bu tür olasılıkların hesabı çarpılarak bulunur. A ve B’nin olasılığı P(A∩B)=P(A).P(B)‘dir.

Örnek:

Bir madeni para ve bir zar birlikte atılır.

Zarın asal sayı ve paranın tura gelme olasılığı kaçtır?

Çözüm:

Soruda verilen olaylar birbirinden bağımsızdır.
Buna göre,

Asal={2,3,5}

P(Asal ∩ Tura)=P(Asal).P(Tura)

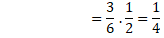
Koşullu Olasılık

A ve B olayları için a olayının olasılığı B olayının gerçekleşmiş olmasına bağlı ise buna koşullu olasılık denir.

Bir olasılık sorusunda “bilindiğine göre” sözcüğü geçiyorsa olasılık koşulludur. Koşullu olasılık sorusu çözülürken “bilindiğine göre” sözcüğü bütün durumları oluşturur.

Örnek:

40 kişilik bir sınıfın 17’si erkektir.
Erkeklerin 6’sı, kızların 5’i gözlüklüdür.

Sınıftan rastgele seçilen bir öğrencinin erkek olduğu bilindiğine göre gözlüksüz olma olasılığı kaçtır?

Çözüm: