Dik Üçgen Konu Anlatımı

Geometri ayt konu anlatımı, Geometri tyt konu anlatımı , Geometri yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Dik Üçgen Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.
Dik Üçgen
Pisagor Teoremi
Pisagor Teoremine göre; bir dik üçgende dik kenarların karelerinin toplamlarının hipotenüsün karesine eşittir.

Pisagor’dan bu yana Pisagor teoremi üzerinde çalışan matematikçiler şöyle bir genellemeye ulaşmıştır:
n pozitif bir doğal sayı olmak üzere;
- a = 2n + 1
- b = 2n2 + 2n
- c = 2n2 + 2n + 1
eşitliklerini sağlayan tüm a, b ve c doğal sayıları, a2 + b2 = c2 eşitliğini de sağlar.
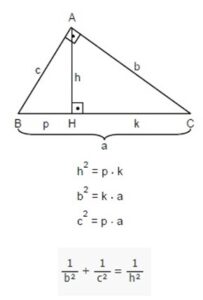
Oklid Teoremi
Bir dik üçgenin dik açının olduğu köşeden karşı kenara indirilen dikme için
Sinüs, Kosinüs, Tanjant, Kotanjant
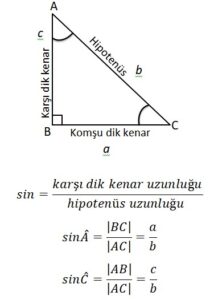
Sinüs
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının sinüsü denir. Bir A açısının sinüsü “sin A” şeklinde gösterilir.
Kosinüs
Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının kosinüsü denir. Bir A açısının kosinüsü “cos A” şeklinde gösterilir.

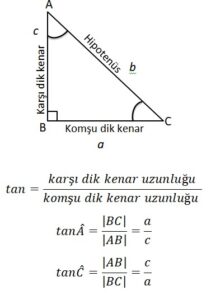
Tanjant
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun komşu dik kenar uzunluğuna oranına o dar açının tanjantı denir. Bir A açısının tanjantı “tan A” şeklinde gösterilir.
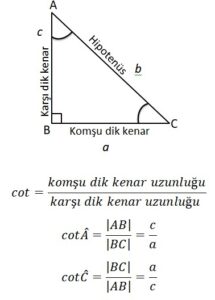
Kotanjant
Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun karşısındaki dik kenar uzunluğuna oranına o dar açının kotanjantı denir. Bir A açısının kontanjantı “cot A” şeklinde gösterilir.
30-60-90 Üçgeni
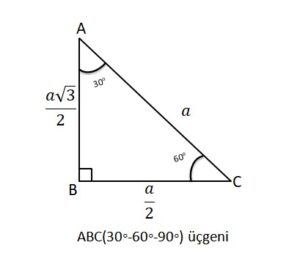
*İç açıları her zaman 30 60 ve 90 olan üçgenlerdir
*30 derecenin karşısındaki kenar uzunluğu hipotenüsün yarısına eşittir.
*60 derecenin karşısındaki kenar uzunluğu ise hipotenüse eşittir. Yani 30 derecenin karşısındaki kenar uzunluğunun iki katıdır.
*90 derecenin karşısındaki kenar uzunluğu ise 60 derece ve 30 derecenin karşısındaki kenar uzunluklarının *toplamına eşittir.

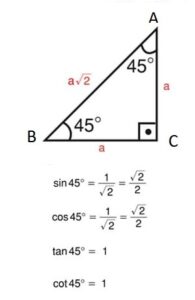
45-45-90 Üçgeni
İkizkenar bir dik üçgenin açıları 45° – 45° – 90° ‘dir. Bu ikizkenar dik üçgenin dik kenarlarının uzunluğunu a kabul edersek hipotenüsün uzunluğunu Pisagor Bağıntısından a2–√ buluruz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.