8. Sınıf Köklü İfadeler Konu Anlatımı

Bu yazımızda sizlere 8. sınıf Köklü İfadeler hakkında bilgilendireceğiz. Aşağıda sizlere başlıklar halinde konularımızı anlattık. Üzerine tıklayarak ulaşabilirsiniz.
Köklü İfadeler
- Kareköklü Sayılara Giriş ve Tam Kare Sayılar
- Kareköklü Bir Sayıyı a√b Şeklinde Yazma
- Kareköklü Sayılarda Katsayıyı Kök İçine Alma
- Kareköklü Sayılarda Sıralama
- Kareköklü Sayılarda Toplama ve Çıkarma İşlemi
- Kareköklü Sayılarda Çarpma ve Bölme İşlemi
- Ondalık Kesirlerin Karekökleri
- Gerçek Sayılar
Kareköklü Sayılara Giriş ve Tam Kare Sayılar
Verilen bir sayının, hangi sayının karesi olduğunu bulma işlemine, karekök alma işlemi denir. Karekök ” √ ” sembolü ile gösterilir. √5, karekök beş olarak okunur. Bir sayının karesi negatif olamayacağından kökün içerisinde negatif sayı bulunmaz. Bir tam sayının karesi olan, diğer bir ifadeyle karekökleri tam sayı olan 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, gibi doğal sayılara tam kare sayılar denir.
Tam Kare Sayılar
Bir tam sayının karesi olan, diğer bir ifade ile karekökü tam sayı olan doğal sayılara tam kare sayılar denir. Tam kare sayılara karesel sayılar da denir.1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 192, 256, 289, … sayıları tam kare sayılardır.

Örnek:
Alanı 49 birim kare olan bir karenin bir kenarı kaç birimdir?
Kenarı ![]() birimdir.
birimdir.
Kareköklü Bir Sayıyı a√b Şeklinde Yazma
Karekök işlemi de bir sayının hangi sayının karesi olduğunu bulmadır. Tam kare sayılar köksüz dışarı çıkarken tam kare olmayan sayılar nasıl dışarı çıkar bulalım.
Kareköklü bir sayıyı ![]() şeklinde yazmak için karekök içindeki çarpanlardan en az biri tam kare sayı olacak şekilde iki sayının çarpımı olarak yazılır. Tam kare olan çarpanların karekökleri, karekök dışına kat sayı olarak yazılır.
şeklinde yazmak için karekök içindeki çarpanlardan en az biri tam kare sayı olacak şekilde iki sayının çarpımı olarak yazılır. Tam kare olan çarpanların karekökleri, karekök dışına kat sayı olarak yazılır.
![]() eşitliği vardır.
eşitliği vardır.
Örnekler:
![]() sayısını
sayısını ![]() şeklinde yazalım.
şeklinde yazalım.
![]() =
=![]()
![]() sayısını
sayısını ![]() şeklinde yazalım.
şeklinde yazalım.
![]()
Kareköklü Sayılarda Katsayıyı Kök İçine Alma
Katsayı karekök içine alınırken katsayının karesi alınarak (kendisi ile çarpılarak) kök içindeki sayı ile çarpılır ve kök içine yazılır.
![]()
Örnekler:
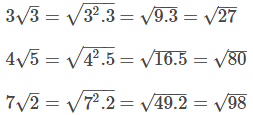
Kareköklü Sayılarda Sıralama
Kareköklü sayılarda sıralama yapmak için katsayılar kök içine alınır. Sonra kök içindeki sayılar karşılaştırılır.
![]()
Örnekler:
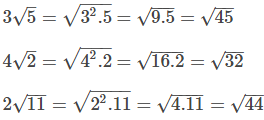
Kareköklü Sayılarda Toplama ve Çıkarma İşlemi
Kareköklü sayılarla toplama ve çıkarma işlemi yaparken, kök içleri aynı olan terimler kendi aralarında toplanır veya çıkarılır. Katsayılar arasında işlem yapılır ve bulunan sonuç ortak köke katsayı olarak yazılır.
Toplama işlemi ![]() eşitliği,
eşitliği,
Çıkarma işlemi ![]() eşitliği ile yazılabilir.
eşitliği ile yazılabilir.
Örnekler:
![]() işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
![]()
![]() işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
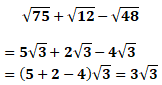
Kareköklü Sayılarda Çarpma ve Bölme İşlemi
Kareköklü sayılarla çarpma işlemi yapılırken varsa katsayılar çarpılarak sonuca katsayı olarak yazılır. Kök içindeki sayılar çarpılarak sonuçta kök içinde yazılır ve kök dışına çıkarma işlemi yapılır.
![]()
Örnek:
![]() işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
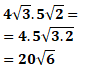
Kareköklü sayılarla bölme işlemi yapılırken varsa katsayılar bölünerek bölüme katsayı olarak yazılır. Sonra kök içindeki sayıların aynı kök içinde yazılır ve bölme işlemi yapılır.![]()
Örnek:
![]() işleminin sonucunu bulalım.
işleminin sonucunu bulalım.
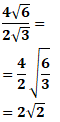
Ondalık Kesirlerin Karekökleri
Ondalık kesirler, rasyonel sayıya çevrildikten sonra karekök dışına çıkartılabilir.
Örnekler:
![]() sayısının değerini bulalım.
sayısının değerini bulalım.
![]()
![]() sayısının değerini bulalım.
sayısının değerini bulalım.
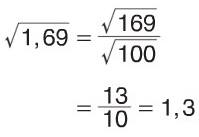
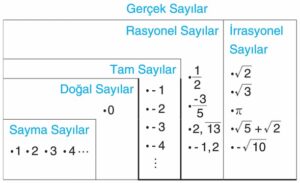
Gerçek Sayılar
Rasyonel Sayılar ve İrrasyonel Sayıların birleşmesiyle oluşan sayı kümesine Gerçek Sayılar denir. Gerçek sayılara Reel Sayılar veya Gerçel Sayılar da denilir. Gerçek sayılar kümesi “R” harfi ile gösterilir.







çok iyi
Güzel ve faydalı olmuş. Keşke bu özetleri bir A4 kağıda odama asabileceğim bir şekidede yayınlasaydınız.
Çok güzel bi konu anlatımı
bende lgs öğrencisiyim konuları çok iyi anlatmışsınız sınavda çok işi yarıyacağını düşünüyorum burdan tüm lgs öğrencilerine başarılar diliyorum
Konularınız çok anlaşılır bir şekilde bende LGS öğrencisiyim okuldan eve gelince konuyu çok iyi pekiştirebiliyorum.Çok teşekkür ederim a
LGS öğrencisiyim çalışmam için faydalı bir konu anlatımı olmuş teşekkürler