8. Sınıf Cebirsel İfadeler ve Özdeşlikler Konu Anlatımı

Bu yazımızda sizlere LGS Matematik konusu olan aynı zamanda 8. sınıf konuları arasında yer alan Cebirsel İfadeler ve Özdeşlikler hakkında bilgilendireceğiz. Aşağıda sizlere başlıklar halinde konularımızı anlattık. Üzerine tıklayarak ulaşabilirsiniz.
Cebirsel İfadeler ve Özdeşlikler
Cebirsel İfadeler
En az bir bir bilinmeyen ve bir işlem içeren ifadelere cebirsel ifadeler denir. Cebirsel ifadelerde sayıları temsil eden harflere değişken ya da bilinmeyen denir.
Bir cebirsel ifadede + veya – işaretleriyle ayrılmış olan ifadelerin her birine terim, bir cebirsel ifadedeki harflere değişken, değişkenin önündeki sayıya katsayı, sadece sayıdan oluşan terime sabit terim denir.
Örnek:
5x-2y+5x-3 cebirsel ifadenin kat sayılar toplamını bulalım.
5x -2y +5x -3
5 – 2 + 5 – 3=5
Cebirsel İfadelerde Çarpma İşlemi
Cebirsel ifadelerle çarpma işlemi yapılırken çarpanlardan birindeki her bir terim ile diğerindeki her bir terim ayrı ayrı çarpılır. Elde edilen sonuçta benzer terimler varsa bunlar arasında toplama çıkarma işlemi yapılarak sadeleştirme yapılır.
Terimli ile 1 Terimli Cebirsel İfadeyi Çarpma
Katsayılar çarpılıp katsayı olarak, bilinmeyenler çarpılıp bilinmeyen olarak sonuca yazılır.
Örnek:
4x ifadesi ile 5x ifadesini çarpalım.
4x’in katsayısı (4) ile 5x’in katsayısı (5) çarpılır. 4.5=15
4x’teki bilinmeyen (x) ile 5x’teki bilinmeyen (x) çarpılır. x.x=x2
Sonuç: 4x.5x = 20x2
1 Terimli ile 2 Terimli Cebirsel İfadeyi Çarpma
Bir terimlideki terim diğer iki terimle sırayla çarpılır ve en son varsa sadeleştirme yapılır.
Örnek:
−4x . ( x + 2 ) işleminde de aynı şekilde x ve +2’yi sırayla −4x ile çarparız.
= ( −4x . x) + ( −4x . 2 )
= (−4x2) + (−8x)
2 Terimli ile 2 Terimli Cebirsel İfadeyi Çarpma
İlk çarpandaki her bir terim ile ikinci çarpandaki her bir terim ayrı ayrı çarpılır. Sonra sadeleştirme varsa yapılır.
Örnek:
( 2x + 3 ) . ( 4x + 1 ) işlemini yapalım.
İlk ifadedeki 2x’i diğer ifadedeki 4x ve +1 ile ayrı ayrı çarpacağız.
Benzer şekilde ilk ifadedeki +3’ü diğer ifadedeki 4x ve +1 ayrı ayrı çarpacağız.
= (2x.4x) + (2x.+1) + (3.4x) + (+3.+1)
= 8x2 + 2x + 12x + 3 [2x ile 12x toplanır]
= 8x2 + 14x + 3
Özdeşlikler
İçindeki değişkenlere verilen bütün gerçek sayılar için doğru olan denklemlere özdeşlik denir. Özdeşlik bir denklemdir. Fakat her denklem özdeşlik değildir.
Özdeşlik ile denklem arasındaki fark; özdeşlikte değişkene verilen her gerçek sayı değerinde eşitlik sağlanır, denklemde ise bazı gerçek sayı değerlerinde eşitlik sağlanır.(Buradaki denklemden kasıt özdeşlik olmayan denklemdir.)
Önemli Özdeşlikler
İki Kare Farkı
![]()
Örnek:
![]()
Örnek:
![]()
olduğuna göre x.y çarpımının sonucu kaçtır?
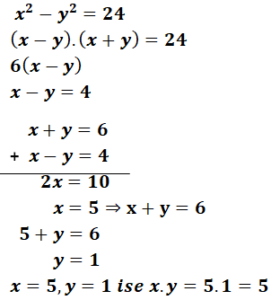
Tam Kare İfadeler
![]()
Bu özdeşlikler düzenlenirse;
![]()
elde edilir.
Örnek:
a-b=3
a.b=4
olduğuna göre ![]() toplamı kaçtır?
toplamı kaçtır?
![]()
Örnek:
a+b=13
a.b=40
olduğuna göre , a-b farkının pozitif değeri kaçtır?
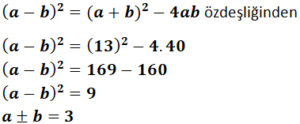
Birkaç Daha Önemli Ödeşlik
İki Kare Toplamı
a2 + b2 = (a − b)2 + 2ab
a2 + b2 = (a + b)2 − 2ab
İki Küp Farkı
a3 − b3 = (a − b) . (a2 + ab + b2)
a3 + b3 = (a + b) . (a2 − ab + b2)
a3 − b3 = (a − b)3 + 3ab . (a − b)
a3 + b3 = (a + b)3 − 3ab . (a + b)
Küp Açılımı
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Cebirsel İfadeleri Çarpanlara Ayırma
Her terimde katsayıların en büyük ortak böleni (EBOB) veya her terimdeki aynı (ortak) çarpan ifadelerinin parantez dışına alınmasına ortak çarpan parantezine alarak çarpanlara ayırma denir.
Ortak Parantez Alma
Bir cebirsel ifadenin her bir terimindeki ortak çarpanların, parantez dışına alınıp terimlerin çarpımı biçiminde yazılmasına bu cebirsel ifadeyi ortak çarpan parantezine almak denir.
a.x + b.x – c.x=x(a+b-c)
Örnek:
3x – 6y = 3(x-2y)
4ax – a = a(4x-1)
Sadeleştirme
Kesirli ifadelerde pay ve paydada ortak çarpanlar varsa bu çarpanların birbirlerini yok etmesi işlemine sadeleştirme denir.
Örnek:
![]()
işleminin sadeleştirilmiş biçimini bulalım.
![]()
Örnek:
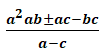
işleminin sadeleştirilmiş biçimini bulalım.
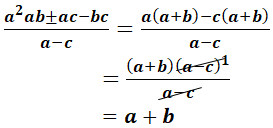
Özdeşliklerden Yararlanılarak Çarpanlara Ayırma
İki Kare Farkı Özdeşliği İle Çarpanlara Ayırma
ki kare farkı şeklinde verilen bir ifadeyi çarpanlarına ayırmak için önce verilen terimlerin karekökleri alınır. İfade bulunan kareköklerin toplamı ile farkının çarpımı şeklinde yazılır.
Örnek:
![]() ifadesinin çarpanlara ayrılmış halini bulalım.
ifadesinin çarpanlara ayrılmış halini bulalım.
![]()
![]()
Tam Kare Şeklinde Verilen Bir İfadeyi Çarpanlara Ayırma
Tam kare şeklinde verilen bir ifadeyi çarpanlarına ayırırken birinci terim ile üçüncü terimin karekökü alınır. Karekök değerlerinin çarpımının iki katı ortanca terime eşit ise birinci terimin karekökü ile üçüncü terimin karekökü, ortanca terimin işaretine bakılarak toplam ya da farkların karesi şeklinde yazılır.
x2 + 2xy + y2 = (x + y).(x + y)
x2 − 2xy + y2 = (x − y).(x − y)
Örnek:
![]() ifadesini tam kare şeklinde yazalım.
ifadesini tam kare şeklinde yazalım.
![]() dir.
dir.







çooooook sağolun,çok iyi
Harika 👍 herkes denemeli
Arkadaşım tavsiye etti. Mükemmelmiş!!👍👍👍👍
Harika. Lgs için mükemmel bir site. Tüm tanıdıklarıma tavsiye ederim.
Çok güzel akıcı !!!
En zorlandığım konu okulda anlamamıştım sayenizde öğrendim, anladım..