6. Sınıf Çember Konu Anlatımı

6. Sınıf Alan Ölçme Konu Anlatımı, 6. Sınıf Alan Ölçme , Alan Ölçme Konu Anlatımı, 6. Sınıf Matematik , 6. Sınıf Matematik Konu Anlatımı, Alan Ölçme
Çember
Çemberin Elemanları
Düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktalar kümesine çember denir. Sabitlenen nokta çemberin merkezidir. Çemberler merkez noktalarına verilen harfler ile adlandırılır.
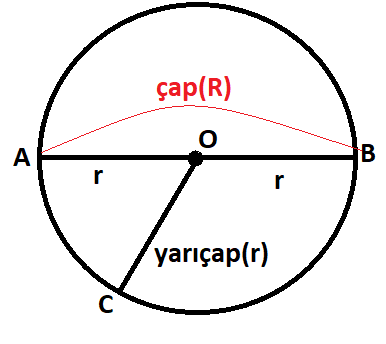 |
Çemberin merkezi ile üzerindeki bir noktayı birleştiren doğru parçalarının her birine yarıçap denir ve r ile gösterilir.
Çemberin merkezinden geçen ve çemberin üzerinde bulunan iki noktayı birleştiren doğru parçasına çap denir ve 2r ya da R ile gösterilir.
|
O merkezli çemberde; [OA], [OB], [OC] yarıçap, [AB] da çaptır.
Pi Sayısı ve Çemberin Çevre Uzunluğu
Bir çember ya da dairenin çevre uzunluğu, çap uzunluğuna bölündüğünde daima aynı sayıyı verir. Bu sayı pi olarak okunur ve “π” sembolü ile gösterilir.
π sayısının kesin değeri bilinmemekle birlikte hesaplamalarda kolaylık sağlaması amacıyla değeri 3, 22/7 ya da 3,14 olarak alınabilir. Verilen örnek içerisinde π sayısının yaklaşık olarak hangi değerde alınacağı belirtilir.
Çemberin uzunluğu: π · çap = π · R = π · 2r
Örnek-1
Yarıçapı 25 cm olan tekerleğin 3 defa döndüğünde kaç cm yol alacağını bulunuz. (π = 3 alınız.)
Çemberin uzunluğu = π · 2r = 3. 2. 25 = 225
3 defa döndüğünden
3 . 225 = 675 cm yol alır.
Örnek-2
Çapı 14 m olan çemberin çevresi kaç metredir? (π =22/7 alınız.)
R = 14
14 /2 = 7
Çemberin uzunluğu = π · R = 22/7 . 14 = 308 / 7 = 44 metredir.
Örnek-3
Bir araba lastiğinin çapı 49 santimetredir. Lastiğin 4 tur attığında alacağı mesafeyi cm cinsinden bulunuz.(π=22/7 alınız.)
Çemberin uzunluğu = π · R = 49. 22/7 = 1078/ 7 = 154
154 . 4 = 616 cm’dir.






