Analitik Düzlemde Temel Dönüşümler Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Analitik Düzlemde Temel Dönüşümler konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Analitik Düzlemde Temel Dönüşümler
Düzlemde Öteleme Dönüşümü
Bir şeklin boyutları bozulmadan yer değiştirmesine öteleme dönüşüm hareketi denir.
Ötelemede biçim, boyut ve yön değişmez. Öteleme dönüşüm hareketi yapılırken x ve y eksenleri boyunca belirtilen yönde, belirtilen birim kadar nokta ötelenir. Sağa ve sola öteleme dönüşüm hareketi x eksenine paralel olarak, yukarı ve aşağı öteleme dönüşüm hareketi ise y eksenine paralel olarak yapılır.
Düzlemde Dönme Dönüşümü
Düzlemde P(x, y) noktasının orijin etrafında a açısı kadar döndürülmesi ile elde edilen nokta Q(x’, y’) ise;
Q=Ra(P)
=(x.cosa-y.sina, x.sina+ycosa) dır.
Burada Rα ya dönme dönüşümü denir. (Rα(P), bir P noktasının α açısı kadar orijin etrafında döndürülmesini simgeler.)
Düzlemin her P noktası için Rα(P) dönmesi yapılabileceğinden Rα: R2 → R2 şeklinde bir dönüşümdür.
-Dönme yalnızca bir noktayı değiştirmez diğer bütün noktaları değiştirir. Değişmeyen noktaya dönme merkezi denir.
-Bir dönme dönüşümünde α açısı kadar döndürelim dendiğinde, döndürme yönü pozitif yani saat yönünün tersinedir. -α açısı kadar döndürme ise negatif yönde yani saat yönünde α açısı kadar döndürmedir.
-Bir P(x, y) noktasının orijin etrafında pozitif yönde 90° döndürülmesiyle elde edilen noktanın koordinatları Q(-y, x) dir.
R90° (x, y) = (-y, x) olur.
-Bir P(x, y) noktasının orijin etrafında negatif yönde 90° (veya pozitif yönde 270°) dönmesiyle elde edilen noktanın koordinatları Q(y, -x) dir.
R-190° (x, y) = (y, -x) olur.
-Bir P(x, y) noktasının orijin etrafında negatif yönde 180° dönmesiyle elde edilen noktanın koordinatları Q(-x, -y) dir.
R180° (x, y) = (-x, -y) dir.
Simetri Dönüşümü
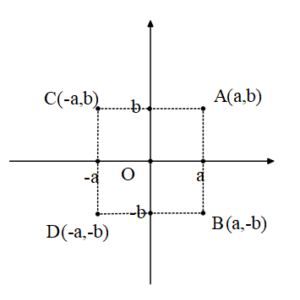
Ox eksenine göre simetriği B(a, —b) (apsis sabit kalır, ordinat işaret değiştirir).
Oy eksenine göre simetriği C(—a, b) (ordinat sabit kalır, apsis işaret değiştirir).
Orijine göre simetriği D(—a, —b) (apsis ve ordinat işaret değiştirir).
Düzlemde Bileşke Dönüşümü

Bir şeklin bir doğru boyunca ötelenip sonra yansımasına veya önce yansıması alınıp sonra ötelenmesine ötelemeli yansıma denir.
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.






