Anlık Değişim Oranı ve Türev Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Anlık Değişim Oranı ve Türev konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Anlık Değişim Oranı ve Türev
- Türev Kavramı
- Sabit Fonksiyon ve xn Biçimindeki Fonksiyonların Türevi
- İki Fonksiyonun Toplamının ve Farkının Türevi
- İkinci Mertebeden Türev
- İki Fonksiyonun Çarpımının ve Bölümünün Türevi
- Bileşke Fonksiyonun Türevi
Türev Kavramı
Bir y=f(x) fonksiyonunda
x bağımsız değişken
y=f(x) bağımlı değişkendir.
1.
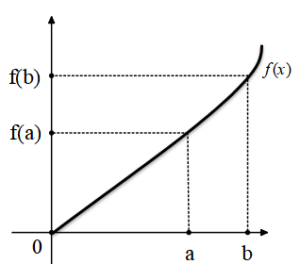
f(x) fonksiyonunun bağımsız değişkeninin a değeri ile b değeri arasında fonksiyonun ortalama değişim hızı
![]()
2.
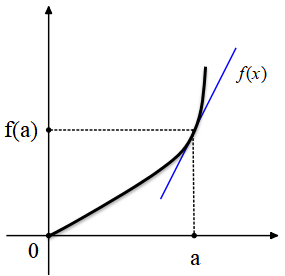
f(x) fonksiyonunun bağımsız değişkeninin a değeri için fonksiyon anlık değişim oranı
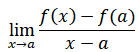
Yani bir fonksiyonun bağımlı değişkendeki değişimin, bağımsız değişkendeki değişime oranının limitine anlık değişim oranı denir.
Anlık değişim oranı aynı zamanda x=a da ki fonksiyonunun grafiğine çizilen teğetin eğimidir.
![]() Bir fonksiyonun anlık değişim oranına fonksiyonun türevi denir. Yani kısaca
Bir fonksiyonun anlık değişim oranına fonksiyonun türevi denir. Yani kısaca
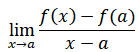
limit değeri,(eğer varsa) f(x) fonksiyonun x=a noktasındaki türevidir ve fonksiyona x=a noktasında çizilen teğetin eğimini verir. f(x) in x=a noktasındaki türevi f'(a) şeklinde gösterilir.
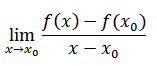
limitinde ![]() dönüşümü yapılırsa
dönüşümü yapılırsa
1.
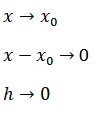
2.
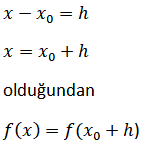





Sabit Fonksiyon ve xn Biçimindeki Fonksiyonların Türevi
1.

2.

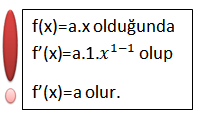

İki Fonksiyonun Toplamının ve Farkının Türevi
f(x) ve g(x) türevlenebilir iki fonksiyon olsun.
1. [f(g)+g(x)]’= f ‘(x)+g'(x)
2. [f(g)-g(x)]’= f ‘(x)-g'(x) olur.
İkinci Mertebeden Türev
Bir f(x) fonksiyonun türevini aldıktan sonra bulduğumuz türev fonksiyonunun bir kere daha türevini alarak f(x)’in ikinci mertebeden türevini bulabiliriz.

İki Fonksiyonun Çarpımının ve Bölümünün Türevi
f(x) ve g(x) türevlenebilir iki fonksiyon olsunlar.
[f(g).g(x)]’= f ‘(x).g(x)+f(x).g'(x) olur.

f(x) ve g(x) türevlenebilir iki fonksiyon olmak üzere g(x)≠0 olsun
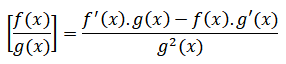 olur.
olur.
Bileşke Fonksiyonun Türevi
f(x) ve g(x) türevlenebilir fonksiyonlar olmak üzere
Bileşke fonksiyon (fog)(x)=f(g(x)) olduğundan;
(fog)'(x)=g'(x).f'(g(x)) bileşke fonksiyonun türevi olur.
12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.






