Matematik ayt konu anlatımı, Matematik tyt konu anlatımı , Matematik yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Binom Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Binom

• Binom Açılımı Özellikleri
• Binom Özdeşliği
• Binom Katsayıları ile Alt küme Sayısı Arasındaki Benzerlik

Bilinen özdeşlikler vardır bunlar;

(x + y)¹ = x + y

(x + y)² = (x + y).(x + y) = x² + 2xy + y²

(x + y)³ = (x + y).(x + y).(x + y) = x³ + 3x²y + 3xy² + y³  

Kuvvet büyüdükçe özdeşliği çarpma işlemi yaparak bulmak zorlaşır. Bu durumda kombinasyon yardımıyla binom açılımını kullanarak özdeşlikleri bulabiliriz.

x ve y sıfırdan farklı ve n bir doğal sayı olmak (x + y)ⁿ ifadesinin x ve y’nin kuvvetleri cinsinden açılımına binom açılımı denir.

Binom açılımında terimleri oluştururken katsayıları kombinasyon yardımıyla hesaplarız. x’in azalan kuvvetlerine göre açılım yaparken x’in üssünü n’den başlayıp her terimde bir azaltırız, y’nin üssünü 0’dan başlayıp her terimde bir arttırırız. Böylece son terimde x’in üssü 0, y’nin üssü n olmuş olur.

Örnek

(x + y)⁴ ifadesinin özdeşini Pascal üçgeninden faydalanarak x’in artan kuvvetlerine göre yazalım.

Terimlerin katsayılarının 1 4 6 4 1 olduğunu Pascal üçgeninin 5. satırından görebiliriz. x’in kuvvetlerini 0’dan 4’e doğru, y’nin kuvvetlerini 4’ten 0’a doğru sırayla terimlere yazarız.

(x + y)⁴ = 1 x⁰ y⁴ + 4 x¹ y³ + 6 x² y² + 4 x³ y¹ + 1 x⁴ y⁰

Katsayılardaki 1’leri, x⁰ ve y⁰ ifadelerini 1’e eşit oldukları için yazmamıza gerek yoktur.

(x + y)⁴ = y⁴ + 4 x y³ + 6 x² y² + 4 x³ y + x⁴

Binom Açılımı Özellikleri

Terim sayısı

(x+y)ⁿ ifadesinin açılımındaki terim sayısı n+1‘dir.

Örnek: (2x + 3y)¹⁰ ifadesinin açılımında 10+1 = 11 terim vardır.

Terimlerdeki üsler toplamı

(x+y)ⁿ ifadesinin açılımındaki her bir terimdeki x ve y değişkenlerinin üsleri toplamı n‘dir.

Örnek: (3x − y)⁸ ifadesinin x’in azalan kuvvetlerine göre açılımındaki baştan 7. terimi inceleyelim.
Bu ifadenin açılımdaki 7. terimi 252x²y⁶ dir. Burdaki x’in ve y’nin üslerini toplarsak 2 + 6 = 8 olduğunu görürüz.

Baştan r+1 inci terim

(x+y)ⁿ ifadesinin x’in azalan kuvvetlerine göre açılımındaki baştan r + 1‘inci terim

Sondan r+1 inci terim

(x+y)ⁿ ifadesinin x’in azalan kuvvetlerine göre açılımındaki sondan r + 1‘inci terim

Ortanca terim

n doğal sayı olmak üzere (x+y)²ⁿ ifadesinin açılımındaki ortadaki terim

Katsayılar toplamı

(x+y)n ifadesinin açılımındaki katsayılar toplamını bulmak için değişkenler yerine 1 sayısı yazılır.

Sabit terim

(x+y)n ifadesinin açılımındaki sabit terimi bulmak için değişkenler yerine 0 sayısı yazılır.

Binom Özdeşliği

Pascal üçgenine dikkat edersek, her bir sayı üstündeki iki sayının toplamı ile oluşmuştur. Mesela 3+1=4  ü oluşturmuştur.

Bunu kombinasyon ile ifade edersek ü oluşturmuştur. Bu durumu şeklinde genelleştirebiliriz. Bu özdeşliğin adı da Binom Özdeşiliği dir.

Örnek:

işleminin sonucu kaçtır?

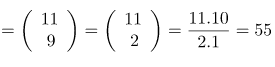
Binom Katsayıları ile Alt küme Sayısı Arasındaki Benzerlik

in açılımındaki katsayılar, n elemanlı bir kümenin 0, 1, 2, … , n elemanlı alt küme sayıları ile aynıdır. Örneğin,

açılımındaki kat sayılar 1, 3, 3 ,1 şeklindedir. 3 elemanlı bir kümenin 0 elemanlı alt küme sayıları  ,,  ve   şeklinde olur.

Bir kümenin tüm alt kümelerinin tane olduğunu biliyoruz. Dolayısıyla;

TYT Matematik Konuları Konu Dağılımı için tıklayınız.

AYT Matematik Konuları Konu Dağılımı için tıklayınız.