Birinci Dereceden İki Bilinmeyenli Eşitsizlikler Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Birinci Dereceden İki Bilinmeyenli Eşitsizlikler konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Birinci Dereceden İki Bilinmeyenli Eşitsizlikler
Kavramlar
> (büyüktür), ≥ (büyüktür veya eşittir), < (küçüktür), ≤ (küçüktür veya eşittir) sembolleri ile yazılan matematiksel ifadelere eşitsizlik denir.
a,b,c ∈ R ve a,b ≠ 0 olmak üzere;
ax + by + c > 0
ax + by + c ≥ 0
ax + by + c < 0
ax + by + c ≤ 0
şeklindeki eşitsizliklere x ve y değişkenine bağlı birinci dereceden iki bilinmeyenli eşitsizlik denir.
Bir eşitsizliğin birinci dereceden iki bilinmeyenli eşitsizlik olabilmesi için iki değişken içermesi ve değişkenlerin kuvvetinin 1 olması gerekir.
Örnek
3x + y > 6 ve y − 3x ≤ 5 eşitsizlikleri birinci dereceden iki bilinmeyenli eşitsizliklerdir.
Birinci dereceden iki bilinmeyenli eşitsizlikleri sağlayan x ve y gerçek sayıları (x, y) sıralı ikilisi olarak yazılır. Bu sıralı ikililerden her biri eşitsizliğin çözüm kümesinin bir elemanıdır.
Örnek
x + y ≥ 3 eşitsizliğini sağlayan (x, y) sıralı ikililerini bulalım.
3 + 0 ≥ 3 doğru olur: (3, 0)
1 + 5 ≥ 3 doğru olur: (1, 5)
Birinci Dereceden İki Bilinmeyenli Eşitsizliklerin Grafikleri
Birinci dereceden iki bilinmeyenli eşitsizliklerin grafikleri koordinat sisteminde bir bölge belirtir. Bu bölge, eşitsizliği sağlayan (x, y) sıralı ikililerinin temsil ettiği noktalardan oluşur.
Örnek
y≤2x−1 eşitsizliğinin çözüm kümesini kartezyen düzlemde gösteriniz.
Çözüm
y=2x−1 doğrusu görüldüğü gibi düzlemi iki bölgeye ayırmaktadır. y< ya da y≤ dendiğinde doğrunun alt tarafı, y> ya da y≥ sorulduğunda da üst tarafını tarayacağız. y≤2x−1 dendiği ve eşitliğin geçerli olduğu noktalar da istendiğinden doğruyu kesikli çizgi ile değil normal çiziyoruz. [note3] y≤ax+b durumunda neden alt tarafı taradığımız anlaşılmadıysa, doğrunun üstünde bir nokta düşünelim. Bu noktanın y si için y=2x−1 ilişkisi geçerlidir. x i değiştirmeden y yi küçültmek için aşağı yönlü gitmeliyiz.
Eşitsizlik Sistemleri
Verilen bir eşitsizlik sisteminin çözümü bulunurken
Her bir eşitsizliğin çözüm aralığı bulunur. Bulunan çözüm aralıklarının kesişim kümesi bulunur. Bu kesişim kümesi eşitsizlik sisteminin çözüm kümesini oluşturur.
Örnek
Aşağıdaki eşitsizlik sisteminin çözüm kümesini analitik düzlemde gösterelim.
y ≥ −2x
2x − 3y < 6
y ≥ −2x eşitsizliğinin çözüm kümesi , 2x − 3y < 6 eşitsizliğinin çözüm kümesi gösterilmiştir.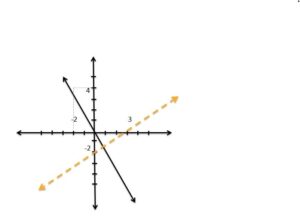
9. Sınıf Matematik Konuları için Tıklayınız
9. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız






