Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak  bilgi sahibi olabilirsiniz. Dik Üçgen ve Trigonometri konusu ile ilgili bütün soruların cevabı sizleri bekliyor…

Dik Üçgen ve Trigonometri

• Pisagor Teoremi
• Oklid Teoremi
• Trigonometri Nedir?
• Sinüs, Kosinüs, Tanjant, Kotanjant
•  30-60-90 Üçgeni
• 45-45-90 Üçgeni

Pisagor Teoremi

Pisagor Teoremine göre; bir dik üçgende dik kenarların karelerinin toplamlarının hipotenüsün karesine eşittir.

Pisagor’dan bu yana Pisagor teoremi üzerinde çalışan matematikçiler şöyle bir genellemeye ulaşmıştır:

n pozitif bir doğal sayı olmak üzere;

• a = 2n + 1
• b = 2n² + 2n
• c = 2n² + 2n + 1

eşitliklerini sağlayan tüm a, b ve c doğal sayıları, a² + b² = c² eşitliğini de sağlar.

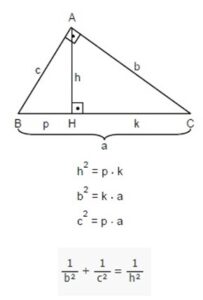
Oklid Teoremi

Bir dik üçgenin dik açının olduğu köşeden karşı kenara indirilen dikme için

Trigonometri Nedir?

Trigonometri kelimesi Yunanca trigōnon (üçgen) ve metron (ölçmek) kelimelerinin birleşmesiyle oluşmuştur. Trigonometri, üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen bir matematik dalıdır. Trigonometri günümüzde ekonomi, fizik ve mühendislik alanlarında sıkça kullanılmaktadır.

Sinüs, Kosinüs, Tanjant, Kotanjant

Sinüs

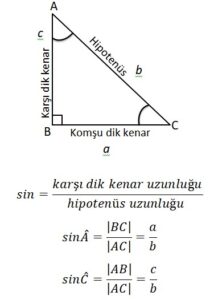
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının sinüsü denir. Bir A açısının sinüsü “sin A” şeklinde gösterilir.

Kosinüs

Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının kosinüsü denir. Bir A açısının kosinüsü “cos A” şeklinde gösterilir.

Tanjant

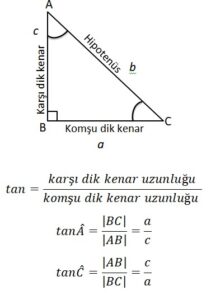
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun komşu dik kenar uzunluğuna oranına o dar açının tanjantı denir. Bir A açısının tanjantı “tan A” şeklinde gösterilir.

Kotanjant

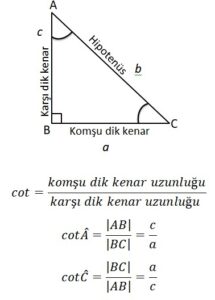
Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun karşısındaki dik kenar uzunluğuna oranına o dar açının kotanjantı denir. Bir A açısının kontanjantı “cot A” şeklinde gösterilir.

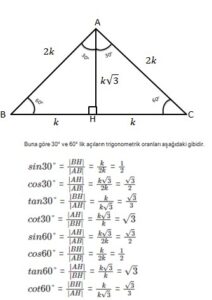
 30-60-90 Üçgeni

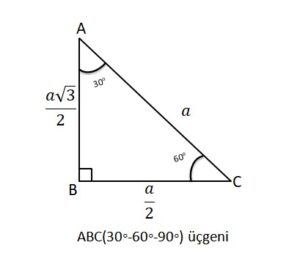
*İç açıları her zaman 30 60 ve 90 olan üçgenlerdir
*30 derecenin karşısındaki kenar uzunluğu hipotenüsün yarısına eşittir.
*60 derecenin karşısındaki kenar uzunluğu ise hipotenüse eşittir. Yani 30 derecenin karşısındaki kenar uzunluğunun iki katıdır.
*90 derecenin karşısındaki kenar uzunluğu ise 60 derece ve 30 derecenin karşısındaki kenar uzunluklarının *toplamına eşittir.

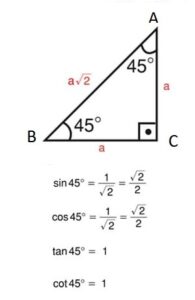
45-45-90 Üçgeni

İkizkenar bir dik üçgenin açıları 45° – 45° – 90° ‘dir. Bu ikizkenar dik üçgenin dik kenarlarının uzunluğunu a kabul edersek hipotenüsün uzunluğunu Pisagor Bağıntısından a2–√ buluruz. Bu kenarları oranlarsak aşağıdaki trigonometrik oranları elde ederiz.

9. Sınıf Matematik Konuları için Tıklayınız

9. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız