İkinci Dereceden Denklemler Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. İkinci Dereceden Denklemler konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
İkinci Dereceden Denklemler
a, b, c ∈ R ve a ≠ 0 olmak üzere,
ax2 + bx + c = 0 şeklindeki eşitliklere ikinci dereceden bir bilinmeyenli denklem denir.
* Denklemi sağlayan x gerçek (reel) sayılarına denklemin kökleri denir.
*Köklerin oluşturduğu kümeye çözüm kümesi (doğruluk kümesi) denir.
*Kökler denklemi sağlar.
Çarpanlara Ayırma Yöntemi İle Kök Bulma
Çarpanlara Ayırma Yöntemi
ax² + bx + c = 0 denklemi f(x) . g(x) = 0 şeklinde yazılabiliyorsa f(x) = 0 veya g(x) = 0 dır.

Δ (Delta) ile Kök Bulma
![]() denkleminin diskriminantı (delta)
denkleminin diskriminantı (delta) ![]() ‘dir.
‘dir.
Δ> 0 ise denklemin farklı iki gerçek (reel) kökü vardır.
Bu kökler x1= ![]() x2=
x2= ![]() dır.
dır.
Δ= 0 ise denklemin birbirine eşit (çakışık , çift katlı) iki gerçek (reel) kökü vardır.
Bu kökler ![]() dır.
dır.
Δ< 0 ise denklemin gerçek(reel) kökü yoktur.
Karmaşık Sayılar
Karmaşık Sayı Tanımı
a, b birer gerçel(reel) sayı olmak üzere z= a+bi biçimindeki bir sayıya karmaşık sayı denir.
z = a + bi karmaşık sayısında a’ya z karmaşık sayısının reel kısmı denir ve Re(z) ile gösterilir, b’ye de z karmaşık sayısının sanal (imajiner) kısmı denir ve Im(z) ile gösterilir.
a, b, c, d birer reel sayı olmak üzere; z1 = a + bi ve z2 = c + di iken z1 = z2 ise a = c ve b = d’dir.
a ve b reel sayılar olmak üzere, a + bi şeklindeki bir karmaşık sayının eşleniği a – bi’dir.
Kökleri Karmaşık Olan Denklemler
Δ≠ 0 ise denklemin farklı iki gerçek (reel) kökü vardır.
![]() denkleminin diskriminantı sıfırdan küçük olduğunda (Δ< 0) karmaşık (sanal) kökleri vardır.
denkleminin diskriminantı sıfırdan küçük olduğunda (Δ< 0) karmaşık (sanal) kökleri vardır.
Bu kökler x1= ![]() x2=
x2= ![]() dır.
dır.
Karmaşık Sayılarda i’nin Kuvvetleri
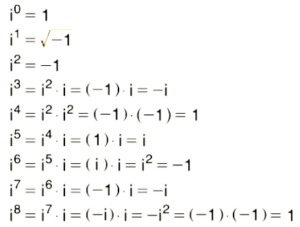
i4n=(i4)n=1n=1 i4n+1=i4n.i1=1 .i=i
i4n+2=i4n.i2=1.-1=-1 i4n+3=i4n.i3=(-1).(-1)=1
Karmaşık Sayılarda Dört İşlem
Toplama ve Çıkarma İşlemi
Toplama ve çıkarmada bir zorluk yok, reel kısımları ayrı, sanal kısımları ayrı topluyoruz ya da çıkarıyoruz.

Karmaşık Sayılarda Çarpma İşlemi
Karmaşık sayılarda çarpma yapılırken dağılma özelliği kullanılır.
Örnek 1:
![]() karmaşık sayısının sonucunu bulalım.
karmaşık sayısının sonucunu bulalım.
Çözüm:
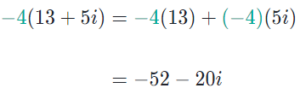
Örnek 2:
![]() sayılarının çarpımı nedir?
sayılarının çarpımı nedir?
Çözüm:
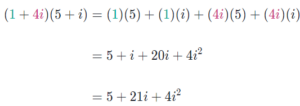
Karmaşık Sayılarda Bölme İşlemi
Karmaşık sayılarla bölme işlemi yapılırken, iki karmaşık sayının birbirine bölümü elde edilmeye çalışılmaktadır. Bölme işlemi yapılırken ters elemandan yardım alınmaktadır. İki karmaşık sayının bölümü, bölenin tersi ile bölünenin çarpımına eşit olduğu bilinmektedir.
Örnek 1:
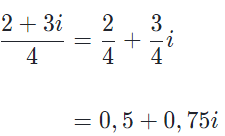
Örnek 2:
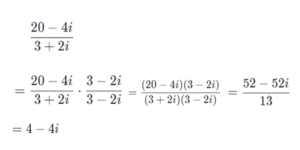







Biraz az örnekli olmuş polinomlara göre ama iyi