Geometri ayt konu anlatımı, Geometri tyt konu anlatımı , Geometri yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Kenarortay Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Kenarortay

• 1. Kural
• 2. Kural
• 3. Kural
• 4. Kural
• 5. Kural
• 6. Kural

Bir üçgende bir köşeyi karşısındaki kenarın orta noktasına birleştiren doğru parçasına o kenara ait kenarortay denir.

1. Üçgenlerde kenarortaylar bir noktada kesişirler. Kenarortayların kesişim noktasına ağırlık merkezi denir.

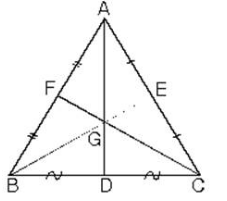
ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarının kesiştikleri G noktasına ABC üçgeninin ağırlık merkezi denir.

Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim uzaklık olacak şekilde böler.

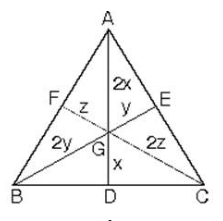
ABC üçgeninde D, E, F noktaları bulundukları kenarların orta noktaları ve G ağırlık merkezi ise

|AG|=2|GD|
|BG|=2|GE|
|CG|=2|GF|

Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.

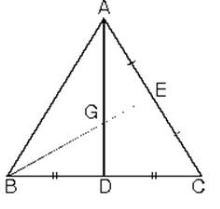
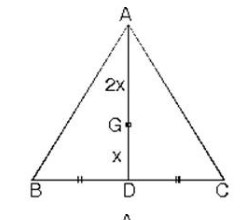
ABC üçgeninde [AD] kenarortay ve |AG| = 2|GD| olduğunda G noktası ağırlık merkezidir.

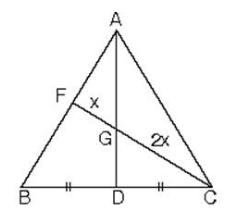
ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG| olduğunda G noktası ağırlık merkezidir.

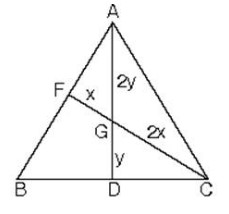
ABC üçgeninde |AG| = 2|GD| ve |CG| = 2|GF| eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.

2. Dik üçgende hipotenüse ait kenarortay (dik köşeden çizilen kenarortay) hipotenüsün yarısına eşittir.

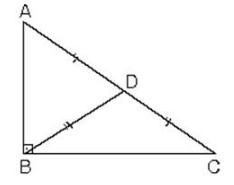
ABC dik üçgeninde [BD] hipotenüse ait kenarortay |AD|=|DC|=|BD|

3. Kenarortayların Böldüğü Alanlar

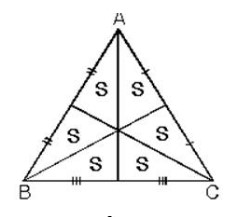
Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.

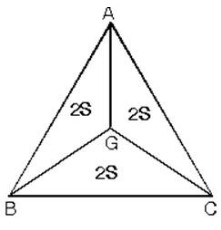
G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

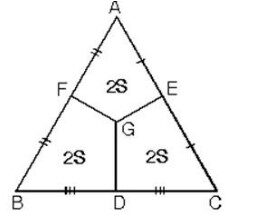
G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

4. ABC üçgeninde kenarortaylar ve orta taban [FE] çizilirse

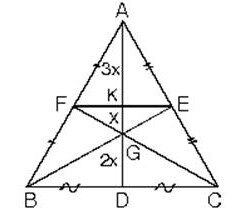
|AK| = 3x
|KG| = x
|GD| = 2x eşitlikleri bulunur.

Bu kuran 312 kuralı olarak da adlandırabilir.

K noktası [AD] kenarortayının orta noktasıdır. Ayrıca [FE] orta taban olduğundan;

[FE] // [BC] 2[FE]=[BC]

ABC üçgeninde kenarortaylar ve [FE] çizildiğinde şekildeki gibi bir alan bölünmesi oluşur.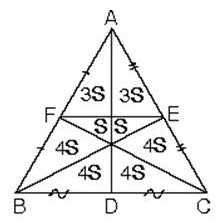

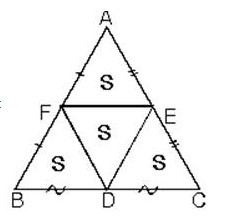
Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.

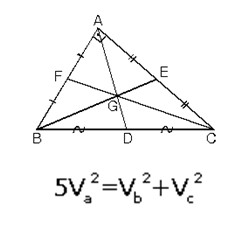
5. Kenarortay Uzunluğu (Kenarortay Teoremi)

ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğu V_a ;

6. Dik Üçgende Kenarortaylar

A açısı 90° olan bir dik üçgende kenarortaylar arasında