Kümelerde İşlemler Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Kümelerde İşlemler konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Kümelerde İşlemler
- Kümelerde Kesişim ve Birleşim İşlemleri
- Kümelerde Fark ve Tümleme İşlemleri
- Küme İşlemleri ile Sembolik Mantık Kuralları Arasındaki İlişki
- İki Kümenin Kartezyen Çarpımı
Kümelerde Kesişim ve Birleşim İşlemleri
Birleşim İşlemi
A ve B herhangi iki küme olsun. A ve B kümelerinin tüm elemanlarının oluşturduğu kümeye A ve B kümelerinin “birleşim kümesi” denir. A ve B kümelerinin birleşim kümesi “A ∪ B” ile gösterilir, “A birleşim B” şeklinde okunur.
Kısaca; A ∪ B = {x | x ∈ A veya x ∈ B} dir.
Örnek
A={a,b,c} ve B={a,2,c} kümelerini Venn şemasında gösterelim.
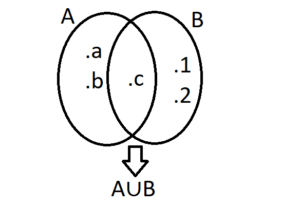
A ∪ B = { 1, 2, a,b,c }
Kesişim İşlemi
A ve B gibi iki kümenin ortak elemanlarından oluşan kümeye A ile B’nin kesişim kümesi denir ve A ∩ B biçiminde gösterilir.
A ve B kümelerinin kesişimi ortak özellik yöntemi ile A ∩ B = { x | x ∈ A ve x ∈ B } şeklinde ifade edilir.
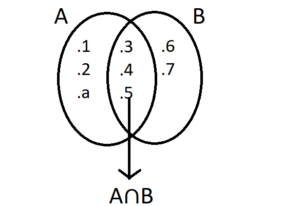
A ∩ B = { 3, 4, 5 }
Örnek
Aşağıda verilen şemanın kesişim ve birleşimlerini gösterelim.
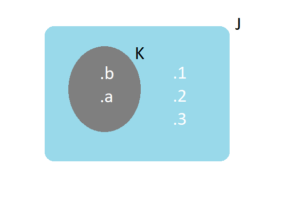
J ∩ K={a,b}
J ∪ K={a,b,1,2,3}
Biri diğerinin alt kümesi olan iki kümenin kesişimi kapsanan kümeye, birleşimi kapsayan kümeye eşittir.
s(K ∩ J) = s(M) = 2
s(K ∪ J) = s(S) =5
Örnek
Aşağıda verilen şemanın kesişim ve birleşim kümlerini yazalım.
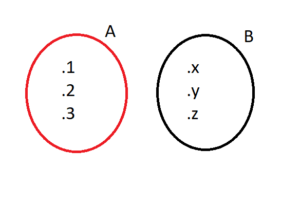
A ∩ B = { }
A ∪ B = {1,2,3,x,y,z }
Kesişimleri boş küme olan kümelere ayrık kümeler denir. Ayrık iki kümenin birleşiminin eleman sayısı, kümelerin eleman sayıları toplamına eşittir.
A ve B ayrık kümeler ise s(A ∪ B) = s(A) + s(B) olur.
Kesişim ve Birleşim İşlemlerinin Özellikleri
Tek Kuvvet Özelliği:
Kesişim işleminin tek kuvvet özelliği vardır.
A ∩ A = A
Birleşim işleminin tek kuvvet özelliği vardır.
A ∪ A = A
Değişme Özelliği:
Kesişim işleminin değişme özelliği vardır.
A ∩ B = B ∩ A
Birleşim işleminin değişme özelliği vardır.
A ∪ B = B ∪ A
Birleşme Özelliği:
Kesişim işleminin birleşme özelliği vardır.
A ∩ ( B ∩ C ) = ( A ∩ B ) ∩ C
Birleşim işleminin birleşme özelliği vardır.
A ∪ ( B ∪ C ) = ( A ∪ B ) ∪ C
Yutan ve Birim Eleman:
Kesişim işleminin yutan elemanı boş kümedir.
A ∩ ∅ = ∅
Birleşim işleminin etkisiz elemanı boş kümedir.
A ∪ ∅ = A
Dağılma Özelliği:
Kesişim işleminin birleşim üzerine soldan ve sağdan dağılma özelliği vardır.
A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )
( B ∪ C ) ∩ A = ( B ∩ A ) ∪ ( C ∩ A )
Birleşim işleminin kesişim üzerine soldan ve sağdan dağılma özelliği vardır.
A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C )
( B ∩ C ) ∪ A = ( B ∪ A ) ∩ ( C ∪ A )
Kümelerde Fark ve Tümleme İşlemleri
E evrensel küme olmak üzere A kümesinde olmayan elemanların oluşturduğu kümeye A kümesinin tümleyeni denir ve A’ ile gösterilir.
A’nın tümleyen kümesi A’ ortak özellik yöntemi ile A’ = { x | x ∉ A ve x ∈ E } şeklinde ifade edilir.
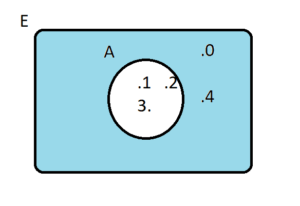
A’ = { 0, 4 }
( A’ )’ = { 1, 2, 3 } = A
A ∩ A’ = ∅
A ∪ A’ = { 0, 1, 2, 3, 4 } = E
s(A) ∪ s(A’) = 3 + 2 = 5 = s(E)
E \ A = { 0, 4 } = A’
E’ = ∅
Tümleme ile İlgili Özellikler
1) ( A’ )’ = A
Bir kümenin tümleyeninin tümleyeni kendisidir.
2) A ∩ A’ = ∅
Bir kümenin tümleyeni ile kesişimi boş kümedir.
3) A ∪ A’ = E
Bir kümenin tümleyeni ile birleşimi evrensel kümedir.
4) s(A) ∪ s(A’) = s(E)
Bir kümenin eleman sayısı ile tümleyeninin eleman sayısının toplamı evrensel kümenin eleman sayısına eşittir.
5) E \ A = A’
Evrensel kümenin bir kümeden farkı o kümenin tümleyenidir.
6) E’ = ∅
Evrensel kümenin tümleyeni boş kümedir.
7) ∅‘ = E
Boş kümenin tümleyeni evrensel kümedir.
Küme İşlemleri ile Sembolik Mantık Kuralları Arasındaki İlişki
| SEMBOLİK MANTIK | KÜMELER |
|---|---|
| 0 | ∅∅ |
| 1 | E |
| ∧ | ∩∩ |
| ∨ | ∪∪ |
| Değili (‘) | Tümleyeni (‘) |
| ≡≡ | = |
| (p’)’ ≡≡ p | (A’)’ = A |
| p ∧ p’ ≡≡ 0 | A ∩∩ A’ = ∅∅ |
| p ∨ p’ ≡≡ 1 | A ∪∪ A’ = E |
| 1 ∧ 0 ≡≡ 0 | E ∩∩ ∅∅ = ∅∅ |
| 1 ∨ 0 ≡≡ 1 | E ∪∪ ∅∅ = E |
| (p ∧ q)’ ≡≡ p’ ∨ q’ | (A ∩∩ B)’ = A’ ∪∪ B’ |
| (p ∨ q)’ ≡≡ p’ ∧ q’ | (A ∪∪ B)’ = A’ ∩∩ B’ |
| p ∧ (q ∨ r) ≡≡ (p ∧ q) ∨ (p ∧ r) | A ∩∩ ( B ∪∪ C ) = ( A ∩∩ B ) ∪∪ ( A ∩∩ C ) |
| p ∨ (q ∧ r) ≡≡ (p ∨ q) ∧ (p ∨ r) | A ∪∪ ( B ∩∩ C ) = ( A ∪∪ B ) ∩∩ ( A ∪∪ C ) |
İki Kümenin Kartezyen Çarpımı
a ve b gibi iki eleman arasına virgül konularak (a, b) şeklinde yazılmasına sıralı ikili denir. (a, b) sıralı ikilisinde a’ya birinci bileşen, b’ye ikinci bileşen denir.
Örnek:
Aynı futbol takımında oynayan Ali, Sertaç ve Tamer, 7, 10 ve 11 numaralı formaları giyebilirler. Bu oyuncuların seçebilecekleri formaları gösteren sıralı ikilileri yazalım.
Çözüm
A kümesi A = { Ali , Sertaç , Tamer }
B kümesi B = { 7 , 10 , 11 }
A X B = { (Ali, 7 ), (Ali, 10), (Ali, 11 ), (Sertaç,7 ), (Sertaç,10 ), (Sertaç,11 ), (Tamer, 7 ), (Tamer, 10 ), (Tamer, 11 ) }
Sıralı ikililerde bileşenlerin sırası önemlidir. (a, b) ≠ (b, a)
Sıralı İkililerin Eşitliği
İki sıralı ikilinin birinci bileşenleri birbirlerine, ikinci bileşenleri de birbirlerine eşit ise bu sıralı ikiler eşittir.
(a, b) ve (c, d) sıralı ikilileri birbirine eşit ise bu durum (a, b) = (c, d) şeklinde gösterilir. Bu durumda a = c ve b = d olur.
Kartezyen Çarpımın Özellikleri
S(A) ; A kümesinin eleman sayısını göstermektedir.
1) s(AxB) = s(BxA) = s(A).s(B)
2) A≠B ise AxB ≠ BxA değişme özelliği yoktur.
3) (AxB)xC = Ax(BxC) birleşme özelliği vardır .
4) Ax(BUC) = (AxB)U(AxC)
5) Ax(B ∩C) = (AxB) ∩ (AxC)
9. Sınıf Matematik Konuları için Tıklayınız
9. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız







elinize sağlık tek anladım