Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak  bilgi sahibi olabilirsiniz. Kümelerde Temel Kavramlar konusu ile ilgili bütün soruların cevabı sizleri bekliyor…

Kümelerde Temel Kavramlar

• Küme Nedir?
• Kümelerin Gösterilişi
• Kümeler
• Alt Küme
• Eşit Küme

Küme Nedir?

Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram “nesneler topluluğu veya yığını” olarak yorumlanabilir. Bu tanımdaki “nesne” soyut ya da somut bir şeydir; fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade eder. Örneğin, “Tüm canlılar topluluğu”, “Dilimiz alfabesindeki harflerin topluluğu”, “Masamın üzerindeki tüm kâğıtlar” tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıktır.

Eleman ve Eleman Sayısı: Kümeyi oluşturan her nesneye o kümenin elemanı denir. Elemanıdır sembolü ∈ ile gösterilir. Elemanı değildir sembolü ∉ ile gösterilir. Bir A kümesinin eleman sayısı sembolle s(A) şeklinde gösterilir.

Kümelerin Gösterilişi

Şema Yöntemi:Küme, kapalı bir eğri içinde her eleman bir nokta ile gösterilip noktanın yanına elemanın adı yazılarak (sol üstteki resim) gösterilir. Bu gösterime Venn Şeması ile gösterim denir.

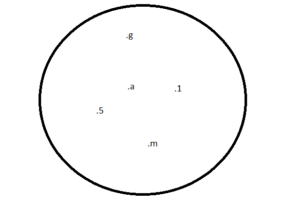Şekilde gördüğünüz küme A kümesi olsun .

Liste Yöntemi: Kümenin elemanları { } sembolü içine, her bir elemanın arasına virgül konularak yazılır.

A kümesi elemanlarını yazmak istersek şu şekilde olur;  A= {g,a,1,m,5}.

Ortak Özellik Yöntemi: Kümeye ait elemanların tek tek yazılmak yerine ortak özelliklerinin yazılmasına ortak özellik yöntemi denir. Ortak özellik yöntemiyle kümelerin gösterimi şu şekildedir: { x | x’lerin ortak özelliği }
Öyle ki anlamına gelen “ | ” sembolü yerine “ : ” sembolü de kullanılabilir.

Örnek

X = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }

Y= { a, b, c, ç }

Z = { 10, 11, 12, 13 }

Kümeler ortak özellik yöntemiyle farklı şekillerde de yazılabilir. Önemli olan yazılan kümenin tam olarak (ne eksik ne fazla) kümenin elemanlarını belirtmesidir.

X = { a | a, bir rakam }

Y = { a : a, Alfabemizin ilk dört harfinden biri }

Z = { a : 9 <a < 14 , a bir doğal sayı }

Kümeler

Boş Küme: Hiçbir elemanı olmayan kümeye boş küme denir. Boş küme { } veya ∅ sembolleri ile gösterilir. Uyarı: {∅} kümesi boş küme olmayıp bir elemana sahiptir.

Eşit Küme ve Denk Küme: Aynı elemanlardan oluşan kümelere eşit kümeler denir. Eleman sayıları eşit olan kümelere denk kümeler denir.

*A kümesi B kümesine eşit ise A = B biçiminde gösterilir.
*C kümesi D kümesine denk ise C ≡ D biçiminde gösterilir.

Not: Eşit olan kümeler ayın zamanda denktir. Fakat denk kümeler eşit olmayabilir.

Evrensel Küme: Üzerinde işlem yapılan tüm kümelere ait elemanları içinde bulunduracak şekilde seçilen kümeye evrensel küme denir. Evrensel küme E harfi ile gösterilir.

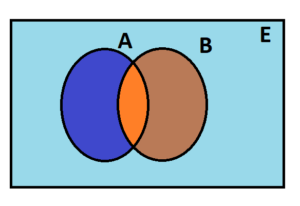
Sonlu ve Sonsuz Küme: Eleman sayısı bir doğal sayı ile ifade edilebilen kümelere sonlu küme, edilemeyen kümelere sonsuz küme denir.

Alt Küme

A ve B iki küme olmak üzere A’nın her elemanı B’nin de elemanı oluyorsa, A’ya B’nin alt kümesi denir. B’ye de A’nın kapsayan kümesi denir. Her küme kendisinin bir alt kümesidir. Boş küme her kümenin alt kümesidir.

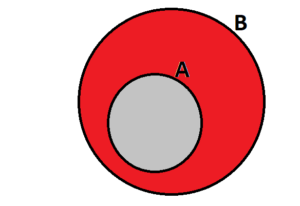
A kümesinin her elemanı aynı zamanda B kümesinin de elemanı ise A kümesi B kümesinin alt kümesidir ve A ⊂ B ya da A ⊆ B ile gösterilir. Bu durumda B kümesi A kümesini kapsar. Bu ifade ise B ⊃ A ya da B ⊇ A ile gösterilir.

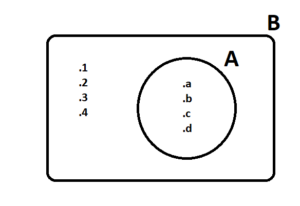
Venn şemasında da görüldüğü gibi A kümesinin her bir elamanı B kümesinin içinde yer almaktadır. Bu durum “A kümesi B kümesinin alt kümesidir (A ⊂ B) ” veya “B kümesi A kümesini kapsar, (B ⊃ A) ” şeklinde ifade edilir.

Özellikleri

*Boş küme her kümenin alt kümesidir. ∅⊂ A
*Her küme evrensel kümenin alt kümesidir. A ⊂ E
*Her küme kendisinin alt kümesidir. A ⊂ A
*A, B ve C kümeleri için A ⊂ B ve B ⊂ C ise A ⊂ C’dir.

Eleman sayısı n olan bir kümenin alt küme sayısı 2ⁿ dir.

Öz Alt Küme Sayısı: Bir kümenin kendisi hariç alt kümelerine öz alt kümeleri denir. n elemanlı bir kümenin öz alt küme sayısı 2n − 1.

Eşit Küme

Elemanları aynı olan kümelere eşit küme denir. A ve B kümelerinin eşitliği A = B ile gösterilir.

K = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 } ve L = { x | x , bir rakam } kümeleri eşit kümelerdir ve bu durum K = L şeklinde gösterilir.

Eşit olmayan A ve B kümeleri A ≠ B şeklinde gösterilir.

9. Sınıf Matematik Konuları için Tıklayınız

9. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız