8. Sınıf Dönüşüm Geometrisi Konu Anlatımı

Bu yazımızda sizlere LGS Matematik konusu olan aynı zamanda 8. sınıf konuları arasında yer alan Dönüşüm Geometrisi hakkında bilgilendireceğiz. Aşağıda sizlere başlıklar halinde konularımızı anlattık. Üzerine tıklayarak ulaşabilirsiniz.
Dönüşüm Geometrisi
Öteleme
Koordinat Sisteminde Öteleme
Bir şekli belirtilen doğrultuda ve birimde ötelemek için şeklin köşe noktaları o doğrultuda istenilen kadar kaydırılır ve birleştirilir.
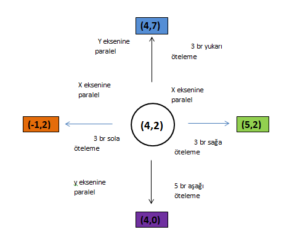
X Eksenine Göre Öteleme
Sağa doğru öteleme yapılıyorsa öteleme miktarı noktanın apsisine (x değeri) eklenir.
A ( X , Y ) noktası x eksenin göre Z birim sağa ötelenirse öteleme sonrası yeni koordinatları A’ ( X+Z , Y ) olur.
Sola doğru öteleme yapılıyorsa öteleme miktarı noktanın apsisinden (x değeri) çıkartılır.
A ( X , Y ) noktası x eksenin göre Z birim sola ötelenirse öteleme sonrası yeni koordinatları A’ ( X–Z , Y ) olur.
Örnek:
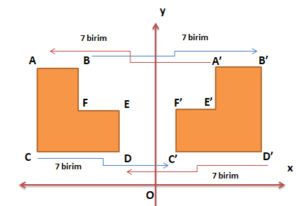
ABCDEF L şekli 7 birim sağa ötelenmiştir. Bu yamuğun köşe noktalarının koordinatlarını incelersek:
A ( – 5 , 6 ) → 7 br sağa → A’ ( 2 , 6 )
B ( – 6 , 2 ) → 7 br sağa → B’ ( 1 , 2 )
C ( – 1 , 2 ) → 7 br sağa → C’ ( 6 , 2 )
D ( – 3 , 6 ) → 7 br sağa → D’ ( 4 , 6 )
Y Eksenine Göre Öteleme
Yukarı doğru öteleme yapılıyorsa öteleme miktarı noktanın ordinatına (y değeri) eklenir.
A ( X , Y ) noktası y eksenin göre Z birim yukarı ötelenirse öteleme sonrası yeni koordinatları A’ ( X , Y+Z ) olur.
Aşağı doğru öteleme yapılıyorsa öteleme miktarı noktanın ordinatından (y değeri) çıkartılır.
A ( X , Y ) noktası y eksenin göre Z birim aşağı ötelenirse öteleme sonrası yeni koordinatları A’ ( X , Y–Z ) olur.
Örnek:
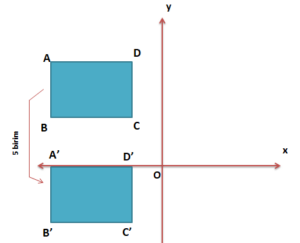
ABCD dikdörtgeni 5 birim aşağı ötelenmiştir. Bu dikdörtgenin köşe noktalarının koordinatlarını incelersek:
A ( – 5 , 2 ) → 5 br aşağı → A’ ( – 5 , – 3 )
B ( – 3 , 2 ) → 5 br aşağı → B’ ( – 3 , – 3 )
C ( – 3 , 5 ) → 5 br aşağı → C’ ( – 3 , 0 )
D ( – 5 , 5 ) → 5 br aşağı → D’ ( – 5 , 0 )
Yansıma
Bir şeklin bir doğruya göre simetrisi alınırsa elde edilen şekil, ilk şeklin doğruya göre yansımasıdır. Yansımada şeklin boyutu ve biçimi değişmez, yeri ve yönü değişir. Doğruya göre simetride şekil ile yansıması eştir.


Koordinat Sisteminde Yansıma
X Eksenine Göre Yansıma – X Eksenine Göre Simetri
Bir şeklin X eksenine göre yansımasını çizmek için şeklin köşe noktalarının x eksenine dik uzaklığı bulunur, x ekseninin diğer tarafına x ekseninden bu kadar uzaklıkta noktalar belirlenir ve birleştirilir. Oluşan şeklin köşe noktalarının koordinatlarına bakılırsa şu görülecektir:
“X” eksenine göre yansıma işleminde, yansıma sonrası apsisler (x değeri) değişmez iken ordinat değeri (y değeri) işaret değiştirir.
A ( X , Y ) noktasının x eksenine göre yansıması olan noktanın koordinatları A’ ( X , – Y ) olur.
Örnek:
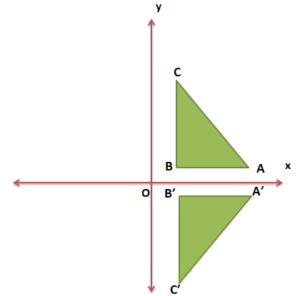
Şekilde ABC üçgeninin x eksenine göre yansıması verilmiştir.
Y Eksenine Göre Yansıma – Y Eksenine Göre Simetri
Bir şeklin Y eksenine göre yansımasını çizmek için şeklin köşe noktalarının y eksenine dik uzaklığı bulunur, y ekseninin diğer tarafına y ekseninden bu kadar uzaklıkta noktalar belirlenir ve birleştirilir. Oluşan şeklin köşe noktalarının koordinatlarına bakılırsa şu görülecektir:
“Y” eksenine göre yansıma işleminde, yansıma sonrası ordinatlar (y değeri) değişmez iken apsis değeri (x değeri) işaret değiştirir.
A ( X , Y ) noktasının y eksenine göre yansıması olan noktanın koordinatları A’ ( – X , Y ) olur
Örnek:
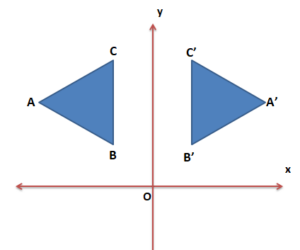
Şekilde ABC üçgeninin x eksenine göre yansıması verilmiştir.






