Bu yazımızda sizlere LGS Matematik konusu olan aynı zamanda  8. sınıf konuları arasında yer alan Üçgenler hakkında bilgilendireceğiz. Aşağıda sizlere başlıklar halinde konularımızı anlattık. Üzerine tıklayarak ulaşabilirsiniz.

Üçgenler

• Üçgende Kenarortay, Açıortay ve Yükseklik
• Üçgenlerin Kenarları Arasındaki İlişkiler
• Üçgenin Açı ve Kenarları Arasındaki İlişkiler
• Pisagor Bağıntısı

Üçgende Kenarortay, Açıortay ve Yükseklik

Kenarortay

Bir üçgenin herhangi bir kenarının orta noktasını, karşı köşe noktası ile birleştiren doğru parçasına üçgenin o kenarına ait kenarortayı denir. “a” kenarına ait kenarortay V_a sembolü ile gösterilir.

. Üçgenlerde kenarortaylar bir noktada kesişirler. Kenarortayların kesişim noktasına ağırlık merkezi denir.

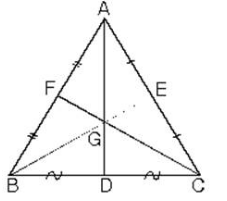
ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarının kesiştikleri G noktasına ABC üçgeninin ağırlık merkezi denir.

Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim uzaklık olacak şekilde böler.

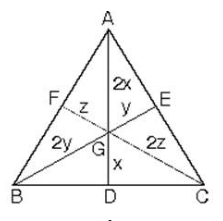
ABC üçgeninde D, E, F noktaları bulundukları kenarların orta noktaları ve G ağırlık merkezi ise

|AG|=2|GD|
|BG|=2|GE|
|CG|=2|GF|

Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.

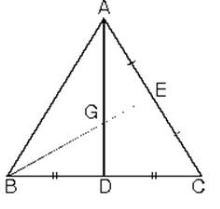
ABC üçgeninde [AD] kenarortay ve |AG| = 2|GD| olduğunda G noktası ağırlık merkezidir.

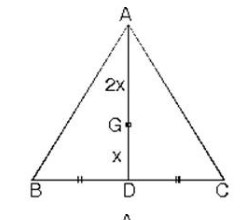
ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG| olduğunda G noktası ağırlık merkezidir.

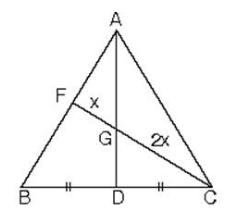
ABC üçgeninde |AG| = 2|GD| ve |CG| = 2|GF| eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.

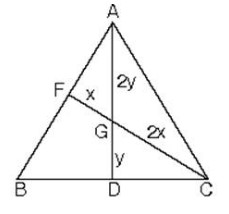
2. Dik üçgende hipotenüse ait kenarortay (dik köşeden çizilen kenarortay) hipotenüsün yarısına eşittir.

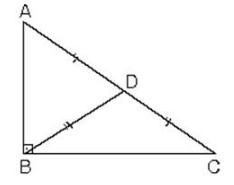
ABC dik üçgeninde [BD] hipotenüse ait kenarortay |AD|=|DC|=|BD|

3. Kenarortayların Böldüğü Alanlar

Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.

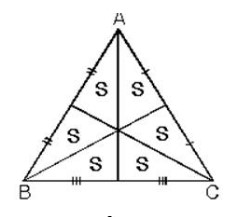
G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

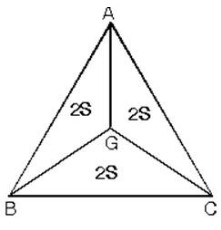
G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

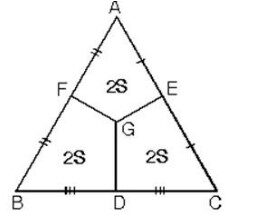
4. ABC üçgeninde kenarortaylar ve orta taban [FE] çizilirse

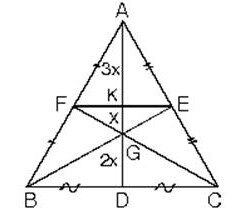
|AK| = 3x
|KG| = x
|GD| = 2x eşitlikleri bulunur.

Bu kuran 312 kuralı olarak da adlandırabilir.

K noktası [AD] kenarortayının orta noktasıdır. Ayrıca [FE] orta taban olduğundan;

[FE] // [BC] 2[FE]=[BC]

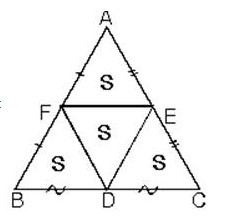
ABC üçgeninde kenarortaylar ve [FE] çizildiğinde şekildeki gibi bir alan bölünmesi oluşur.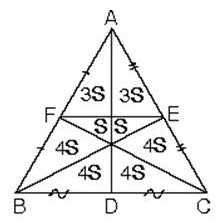

Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.

5. Kenarortay Uzunluğu (Kenarortay Teoremi)

ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğu V_a ;

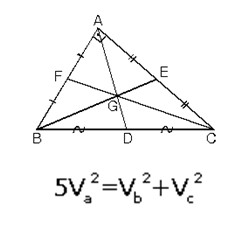
6. Dik Üçgende Kenarortaylar

A açısı 90° olan bir dik üçgende kenarortaylar arasında

Açıortay

Üçgenin bir köşesindeki açıyı iki eş parçaya ayıran doğru parçasına açıortay denir. Açıortay “n” sembolü ile gösterilir.

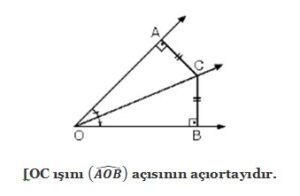
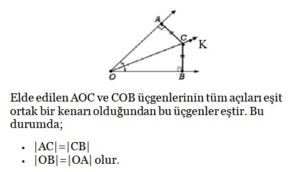
Açıortay Teoreminin İspatı

Üçgende İç Açıortay

Bir üçgenin bir iç açısını iki eş açıya ayıran ışına o üçgenin iç açıortayı denir. Bir üçgende iç açıortaylar tek noktada kesişir.

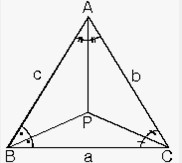
Bir üçgende iç açıortayların kesişim noktası üçgenin iç teğet çemberinin merkezidir.

Üçgende İç Açıortay Teoremi

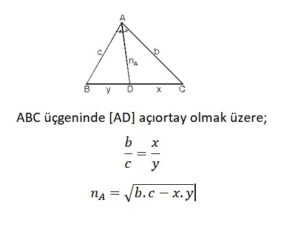
Üçgende Dış Açıortay 

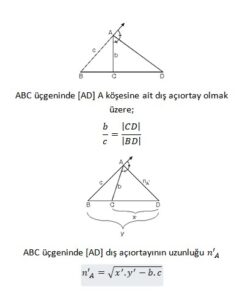
Yükseklik

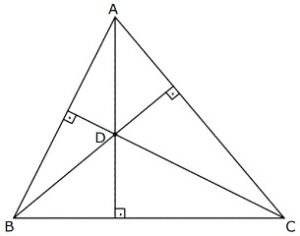
Üçgenin bir köşesinden karşısındaki kenara veya uzantısına çizilen dik doğru parçasına o kenara ait yükseklik denir. Yüksekliklerin kesiştiği nokta üçgenin diklik merkezidir.

İkiz Kenar Üçgende Yükseklik

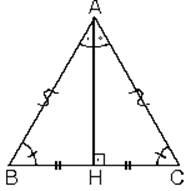
İkizkenar üçgenlerde eşit olmayan kenara indirilen dikme üçgeni iki eş üçgene ayırır.

1. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.

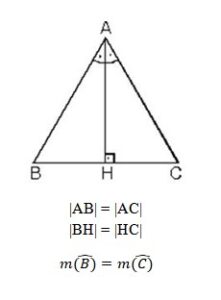
2. Bir üçgende, açıortay aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.

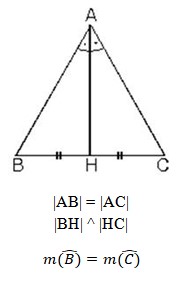
3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.

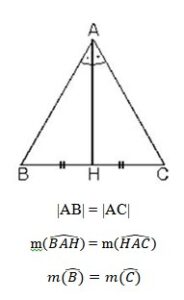
4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.

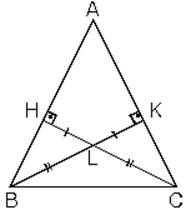
Eşkenar Üçgende Yükseklik

1. Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir.

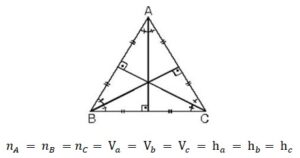
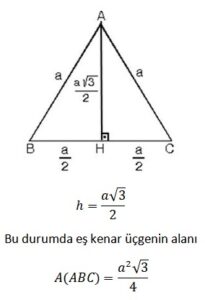
2. Eşkenar üçgenin bir kenarına a dersek yükseklik;

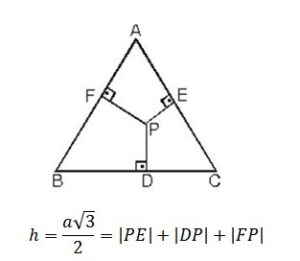
3. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende;

Üçgenlerin Kenarları Arasındaki İlişkiler

Üçgen Eşitsizliği

Bir üçgende bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak değerinden büyüktür. Bu eşitsizliğe üçgen eşitsizliği denir.

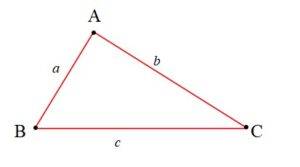
b-c < a < b+c

a-c < b < a+c

a-b < c < a+b

Üçgenin Açı ve Kenarları Arasındaki İlişkiler

1. Bir üçgende ölçüsü büyük olan açının karşısındaki kenar uzunluğu, ölçüsü küçük olan açının karşısındaki kenar uzunluğundan daha büyüktür. Yani büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.

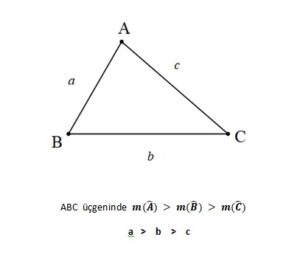
Tersi de geçerlidir. Uzun kenarı gören açı kısa kenarı gören açıdan daha büyüktür. İkizkenar üçgenden de bildiğimiz gibi eşit açıların karşılarındaki kenarlar eşittir.

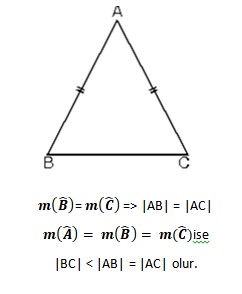
2. Bir üçgende herhangi bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük farkının mutlak değerinden büyüktür. ABC üçgeninde,

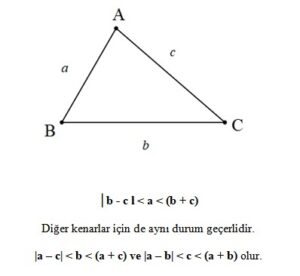
3.  Dik, dar ve geniş açılı üçgenlerde kenarlar arasındaki ilişkiler.

Bir dik üçgende kenarlar arasında Pisagor Teoremi b² = a² + c² bağıntısı vardır.

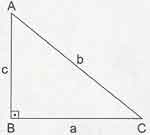
 Dar açılı üçgende b ve c sabit tutulup A açısı küçültülürse a da küçülür.

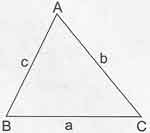m(Â) < 90°   a2 < b2  + c2

Geniş açılı üçgende a ve c sabit tutulup B açısı büyütülürse b’ de büyür.

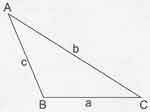m(B) > 90°  b2 > a2 + c2

4. Çeşitkenar bir üçgende aynı köşeden çizilen yükseklik, açıortay ve kenarortay uzunluklarının sıralanması,

|AB| = h_a ; yükseklik

|AD| = n_A ; açıortay

|AK| = V_a ; kenarortay

Olmak üzere; h_a< n_A <V_a     şeklinde sıralama vardır.

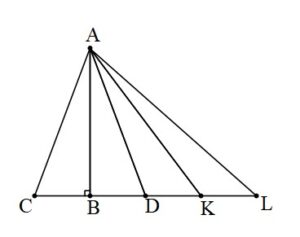
5. Çeşitkenar bir üçgende, açı, açıortay, kenarortay ve yükseklik arasındaki sıralama; ABC üçgeninde a, b, c kenar uzunluklarıdır.

m(A) > m(B) > m(C) olduğunu varsayalım. Bu durumda üçgende;

Kenarlar :a > b > c

Yükseklikler :     h_a < h_b < h_c

Açıortaylar :       n_A < n_B < n_C

Kenarortaylar : V_a < V_b < V_c şeklinde sıralanırlar.

Pisagor Bağıntısı

Pisagor Teoremine göre; bir dik üçgende dik kenarların karelerinin toplamlarının hipotenüsün karesine eşittir.

Pisagor’dan bu yana Pisagor teoremi üzerinde çalışan matematikçiler şöyle bir genellemeye ulaşmıştır:

n pozitif bir doğal sayı olmak üzere;

• a = 2n + 1
• b = 2n² + 2n
• c = 2n² + 2n + 1

eşitliklerini sağlayan tüm a, b ve c doğal sayıları, a² + b² = c² eşitliğini de sağlar.

LGS Matematik için Tıklayınız