Polinomlar Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Polinomlar konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Polinomlar
Polinom Tanımı
![]() biçimindeki ifadelere x değişkenine göre düzenlenmiş reel katsayılı polinom (çok terimli) denir.
biçimindeki ifadelere x değişkenine göre düzenlenmiş reel katsayılı polinom (çok terimli) denir.
Burada a0, a1, a2, a3 …, an reel sayılarına polinomun katsayıları, a0, a1.x, a2.x2, a3.x3,…., an.xn ifadelerine polinomun terimleri olarak adlandırılır.
an.xn terimindeki an sayısına terimin katsayısı, x’in kuvveti olan n sayısına terimin derecesi olarak adlandırılır.
Derecesi en büyük olan terimin derecesine polinomun derecesi denir ve der [P(x)] ile gösterilir. Derecesi en büyük olan terimin katsayısı ise polinomun baş katsayısı olarak adlandırılır.
Polinomlar katsayılarına göre isimlendirilir. Katsayılarımız reel sayı ise reel katsayılı polinomlar, rasyonel sayı ise rasyonel katsayılı polinomlar, tam sayı ise tam katsayılı polinom denir.
Örnek:
![]()
Çünkü x’in üssü doğal sayı olmalıdır.

![]() olmak üzere.
olmak üzere.
![]() in her birine polinomun terimlerinin katsayıları denir.
in her birine polinomun terimlerinin katsayıları denir.
![]() in her birine polinomun terimleri denir.
in her birine polinomun terimleri denir.
Polinomun terimlerinden biri olan a2x2 teriminde x in kuvveti olan 2 ye bu terimin derecesi denir.
Polinomu oluşturan terimler içerisinde derecesi en büyük olan terimin katsayısına polinomun baş katsayısı, bu terimin derecesine de polinomun derecesi denir ve der [p(x)] ile gösterilir.
Değişkene bağlı olmayan terime polinomun sabit terimi denir.
Örnek:
![]()
Polinomunun katsayıları: 3, -2, 1, 5, 1 dir.
Polinomunun derecesi: 4 tür.
Polinomun Baş Katsayısı: 3 tür.
Sabit Terimi: 1 dir.
Tek dereceli terimlerin katsayıları: -2, 5 tir.
Çift dereceli terimlerin katsayıları: 3, 1, 1 dir.
Not: x=0 yazılarak polinomun sabit terimi, x=1 yazılarak, polinomun katsayılar toplamı bulunur. P(x) in sabit terimi P(0), katsayılar toplamı da P(1) dir.
Örnek:
![]() olduğuna göre, P(x + 3)’ün katsayılar kaçtır?
olduğuna göre, P(x + 3)’ün katsayılar kaçtır?
Çözüm:
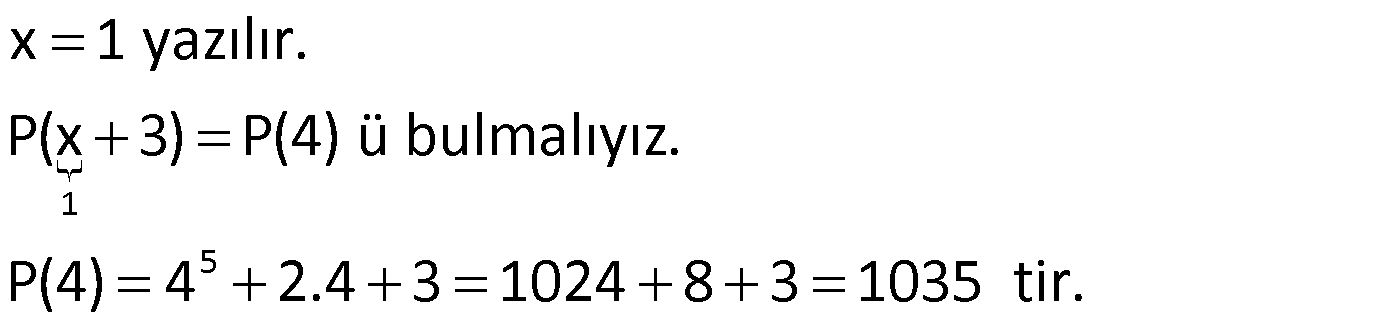
Not: Polinomun çift dereceli terimlerin katsayılar toplamı:
![]()
Tek dereceli terimlerinin katsayıları toplamı:
![]()
Örnek:

Sabit Polinom
c ϵ R ve c≠0 ( c, 0 dan farklı bir reel sayı ) olmak üzere P(x) = c biçimindeki polinomlar sabit polinom olarak adlandırılır. Sabit polinomun derecesi 0 dır.
Örnek: P(x)=5
Sabit polinomun derecesi 0 dır.
Sıfır Polinomu
P(x) = 0 biçimindeki polinomu sıfır polinomu olarak adlandırılır. Sıfır polinomunun derecesi tanımsızdır.
Her polinom bir fonksiyondur. Fakat her fonksiyon polinom olmayabilir.Buna göre, fonksiyonlarda yapılan işlemler polinomlarda da yapılır.
Polinomun Eşitliği
Aynı dereceli en az iki polinomun eşit dereceli terimlerinin katsayıları birbirine eşit ise bu polinomlara eşit polinomlar denir.
P(x) polinomunun katsayıları toplamı P(1) dir.
P(x) polinomunda sabit terim P(0) dır.
Herhangi bir polinomda; katsayılar toplamı bulunurken o polinomda değişkenler yerine 1 yazılır. Sabit terim bulunurken o polinomda değişkenler yerine 0 (sıfır) yazılır.P(ax + b) polinomunun; katsayıları toplamıP(a + b) ve sabit terimi P(b) dir.
Örnek:
P(x) = ax2 + (b – 3)x + 5
Q(x) = – 3x2 + 5x + c + 7
P(x) = Q(x) olduğuna göre a,b,c nin alabileceği değeri bulunuz.
P(x) = Q(x) ise ax2 + (b – 3)x + 5 = – 3x2 + 5x + c + 7
a = – 3
b – 3 = 5
b = 8
c + 7 = 5
c = – 2
Polinomlarda Dört İşlem
Polinomlarda Toplama Çıkarma İşlemi
Polinomlarda toplama çıkarma yapılırken, aynı dereceli terimlerin katsayıları toplanır ya da çıkarılır.

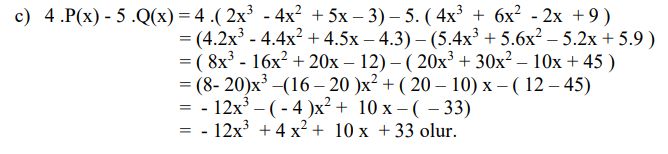
Not: Dereceleri farklı olan iki polinomun toplamının veya farkının derecesi, derecesi büyük olan polinomun derecesine eşittir.
Polinomlarda Çarpma İşlemi
P(x) ile Q(x) çarpılırken, P(x)’in bütün terimleri Q(x) in bütün terimleri ile çarpılır. Ortaya çıkan terimlerin toplamı, çarpımın sonucunu verir.
Örnek:

Polinomlarda Bölme İşlemi

der [ P(x) ] ≥ der [ Q(x)]
der [K(x) ] < der [ Q(x) ]
P(x) = Q(x) . B(x) + K(x)
der [ K(x) ] < der [B (x) ] ise Q (x ) ile B(x) in yer değiştirmesi kalanı değiştirmez.
K (x) = 0 ise P(x) polinomu Q(x) polinomuna tm olarak bölünür. Bu durumda P(x) in çarpanlarından biri Q(x) polinomudur.
Örnek-1:
![]() Q (x)= x-1 polinomuna bölelim.
Q (x)= x-1 polinomuna bölelim.
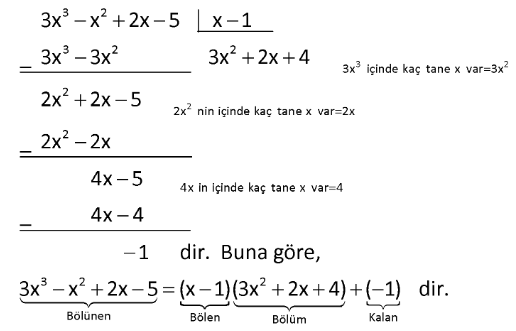
Örnek-2:
![]() polinomunun (x – 2) ile bölümünden kalan kaçtır.
polinomunun (x – 2) ile bölümünden kalan kaçtır.

Polinomlarda Bölme İşleminin Yapılışı
Polinomlarda bölme işlemi sayılarda bölme işlemine benzer şekilde yapılır. Bunun için sırasıyla aşağıdaki işlemler yapılır.
⇒ Bölünen ve bölen polinomlar x değişkeninin azalan kuvvetlerine göre sıralanır.
⇒ Bölünen polinomun soldan ilk terimi , bölen polinomun soldan ilk terimine bölünür. Çıkan sonuç bölümün ilk terimi olur.
⇒ Bulunan bu sonuç bölen polinomun bütün terimleri ile çarpılarak aynı dereceli terimler alt alta gelecek şekilde bölünen polinomun altına yazılır.
⇒ Bölünenin altına yazılan çarpım polinomu , bölünenin polinomdan çıkarılır.
⇒ Yukarıdaki işlemlere , kalan polinomun derecesi , bölen polinomun derecesinden küçük oluncaya kadar devam eder.
Örnek:

Örnek:
P(x) = 4x3– 3x2 + x + 2 polinomunun ve Q(x) = x + 1 polinomu ile bölümünden bulunan kalanı ,bölüm polinomunu bulmadan bulunuz.
Çözüm:
K(x) polinomunu bölme yapmadan bulmamız isteniyor.
P(x) = Q(x) . B(x) + K(x) dir.
Der[ K(x)] < der[ Q(x) ] olacağı için, K(x) = c olur. ( c ∈ R )
P(x) = ( x + 1) . B(x) + c eşitliğinde x yerine -1 yazalım.
P(x) = ( -1 + 1) . B(- 1) + c
P(-1) = c bulunur.
P(-1 ) = 4 (- 1)3 – 3( -1)2– 1 + 2
P(-1 ) = 4 . (- 1) – 3 – 1 + 2
P(-1 ) = – 4 -3 – 1 + 2
P(-1 ) = – 6 olur.







Güzel
İşime yaradı teşekkürler
Çok iyi ve basit anlatmışsınız emeğinize sağlık.
çok karışık
Hatalar çok fazla
Daha özenle anlatılabilirdi