Matematik ayt konu anlatımı, Matematik tyt konu anlatımı , Matematik yks konu anlatımı… Merhaba arkadaşlar sizlere bu yazımızda Problemler Konu Anlatımı hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi edinebilirsiniz.

Problemler

• Sayı- Kesir Problemleri
• Yaş Problemleri
• İşçi-Havuz Problemleri
• Hareket Problemleri
• Yüzde, Kâr-Zarar ve Faiz Problemleri
• Karışım Problemleri

Sayı- Kesir Problemleri

Sayı Problemleri

Sayı problemlerini çözerken yapılması gereken  işlemler aşağıdaki gibidir.

– Problemlerde verilenlerle  istenenler belirlenir.
– Verilenler matematiksel ifadeye çevrilir ve elde edilen ifadeler, denklem çözme metotlarından yararlanılarak çözülür.
– Bulunan sonucun problemde istenen olup olmadığı kontrol edilir.

Matematiksel ifadeye çevirme yöntemleri:

Herhangi bir x sayısı için;

Herhangi iki sayı x ve y olsun.

Ardışık sayılardan en küçüğü x olsun.

Bilinmeyenler birbiri cinsinden yazılabilir.

Örnek:

2 katının 3 eksiği 33 e eşit olan sayı kaçtır?

Çözüm:
İstenilen sayı x olsun

2.x-3=33
2.x=33+3
2x=36
x=18

Örnek:

Toplamları 18, farkları 44olan iki sayıdan büyük olan sayı kaçtır?

Çözüm:

Toplamları x+y=18
Farkları      x-y=44

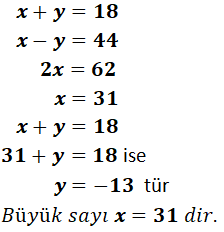
Örnek:

Kendisinin 2 fazlası ile 2 eksiğinin çarpımı, 2 eksiğinin karesine eşit olan sayı kaçtır?

Çözüm:

Bu sayı x olsun. Kendisinin 2 fazlası ile 2 eksiğinin çarpımı (x+2).(x-2)

(x-2).(x+2)=

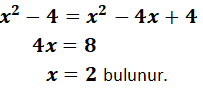
Örnek:

200 gram toz şeker x TL , 350 gram toz şeker (2x-1) TL dir.

Buna göre yarım kilo toz şeker kaç TL dir?

Çözüm:

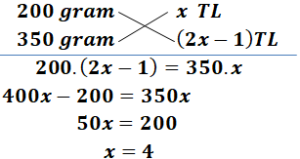
Yarım kilo 500 gramdır.

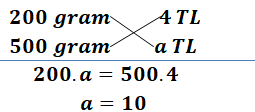
Kesir Problemleri

Kesir problemlerini çözerken , sayı problemlerindeki işlemler kullanılarak denklemler kurulur ve bu denklemler çözülüp sonuca ulaşılır.

Burada, verilenleri matematiksel ifadeye çevirme yöntemleri;

Herhangi bir x sayısı için

Örnek:

Bir sayının inin 2 fazlası aynı sayının 4 eksiğine eşittir.

Buna göre bu sayı kaçtır?

Çözüm:

Bu sayı x olsun

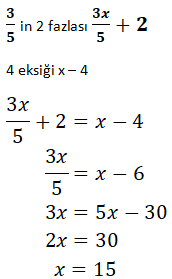
Örnek:

Bir telin orta noktası işaretlendikten sonra bir ucundan unu kesilince orta nokta 4 cm kaymaktadır.

Buna göre telin kesilmeden önceki boyu kaç cm dir?

Çözüm:

bir telin bir ucundan kesilen miktarın yarısı kadar orta nokta kayar. Telin tamamı 10x olsun u kesildiğinden x cm kesilmiştir. buradan orta nokta cm kayıyor.

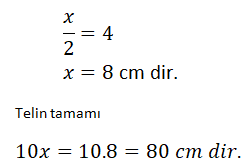
Yaş Problemleri

Yaş problemlerini çözerken; sayı ve kesir problemlerinde yapılması gereken denklem kurma ve denklem çözme metotlarınım yanı sıra , aşağıdaki özelliklerden yararlanılır.

Örnek:

Bir annenin yaşı 34, kızının yaşı 6 dır.

Buna göre kaç yıl sonra annenin yaşı kızının yaşının 4 katı olur?

Çözüm:

x yıl sonra annenin yaşı kızının yaşının 4 katı  olsun.

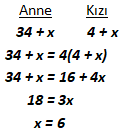
Örnek:

Emel’in yaşının Kemal’in yaşına oranı tit.

3 yıl sonra bu oran olduğuna göre Kemal, Emel’den kaç yaş büyüktür?

Çözüm:

Emel’in yaşının Kemal’in yaşına oranı ise

İşçi-Havuz Problemleri

İşçi Problemleri

İşçi ve havuz problemlerinde birim zamanda yapılan iş miktarları dikkate alınarak denklemler oluşturulur. İşçi ve havuz problemleri ayrıca orantı kurularak da çözülebilir.

Bir işi, birinci işçi tek başına a günde, ikinci işçi tek başına b günde, ikisi birlikte c günde yapabiliyorsa

Örnek:

Burak bir işi 15 günde Sefa aynı işi 30 günde bitirebilmektedir.

Bu işi birlikte çalışarak kaç günde  bitirirler?

Çözüm:

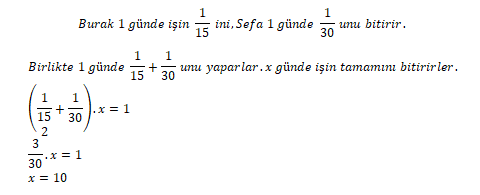
Havuz Problemleri

Boş bir havuzu, 1. musluk x saatte dolduruyor, 2. musluk y saatte boşaltıyor ve iki musluk beraber z saatte dolduruyorsa

Burada havuz doldurma işi pozitif seçildiğinden havuzu boşaltma işi negatif olur.

Örnek:

Bit havuzu en üstte bulunan A musluğu boşken 12 saatte dolduruyor. Havuzun tabanında bulunan B musluğu da dolu havuzu 48 saatte boşaltmaktadır.

Havuz boş iken iki musluk aynı anda açıldığında havuzun tamamı kaç saatte dolar?

Çözüm:

Örnek:

Bir havuzun üstünde bulunan A ve B muslukları sırayla boş havuzu 12 ve 24 saatte doldurmaktadırlar.

Boş olan havuzda önce A musluğu 3 saat açık bırakıldıktan sonra B musluğu da açılırsa  havuzun kalan kısmı kaç saatte dolar?

Çözüm:

Hareket Problemleri

Hareket problemleri; hareket eden bir aracın veya hareketinin, sabit bir hızla belirli sürede aldığı yol miktarının hesaplanması esasına dayanır.

Bu hesapmalama;

Yol =Hız x Zaman

formülü ile gerçekleşir.

X=Yol
V= Hız
t: Zaman(Süre) olmak üzere

X=V.t olacaktır.

Hareket problemlerinde verilerin birimleri;

Örnek:

Bir otomobil 120 km/sa hızla 6 saatte aldığı yolu 90 km/sa hızla kaç saatte alır?

Çözüm:

Yüzde, Kâr-Zarar ve Faiz Problemleri

Yüzde Problemleri

Yüzde, oran yardımıyla ifade edilebilen bir kavramdır ve % ile gösterilebilir. Buradaki oranda; yüzde oranı paya 100 ise paydaya yazılır.

Örnek:

Hangi sayının %20 si ile %12 sinin toplamı 96’ya eşittir?

Çözüm: 

İstenen sayı x olsun

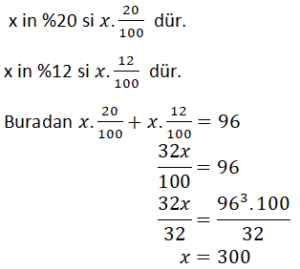
Kâr-Zarar Problemleri

Alış Fiyatı: Bir malın alındığı fiyata alış fiyatı denir.
Maliyet: Belirli bir fiyata alınan bir mal için yapılan taşıma, paketleme, depolama, işçilik vb… gibi harcamalar toplamı ile alış fiyatı toplamına maliyet denir.
Etiket Fiyatı: Bir malın üzerinde yazan satış fiyatına etiket fiyatı denir.
Satış Fiyatı: Bir malın satıldığı fiyata satış fiyatı denir.
Kâr: Bir malın satış fiyatı > maliyet fiyatı ise satış fiyatının maliyet fiyatından farkına kâr denir.
Zarar: Bir malın maliyet fiyatı > satış fiyatından ise maliyet fiyatının satış fiyatından farkına zarar denir.
İskonto: Bir malın satış fiyatının azaltılmasına iskonto denir.
Ciro: Satış sonunda ele geçen paraya ciro denir.

Bir malın % x karla satılması, maliyetinin % x fazlasına satılması demektir.
Bir malın % x zararla satılması maliyetinin % x eksiğine satılması demektir.

A: Bir malın alış fiyatı, mal oluş fiyatı veya maliyeti
S: Bir malın satış fiyatı veya etiket fiyatı
K: Kâr
Z: Zarar

Kâr= Satış Fiyatı-Alış Fiyatı
K=S-A

Zarar=Alış Fiyatı- Satış Fiyatı
Z=A-S

Aksi belirtilmedikçe, kâr-zarar yüzdeleri alış fiyatı üzerinden hesaplanır.

şeklinde hesaplanır.

İndirim ya da zam aksi belirtilmedikçe, satış fiyatı üzerinden hesaplanarak yapılır.

Örnek:

Bir spot mağazasında 1200 TL satılan bir buzdolabı Ahmet pazarlık yaparak 1020 TL’ye indirip satın almıştır.

Buna göre Faruk satış üzerinden yüzde kaç indirim almıştır?

Çözüm:

Örnek:

Satış etiketinde 1200 TL+ KDV yazılı olan bir bilgisayarın KDV oranı %18 dir.

Buna göre bilgisayarın KDV dahil fiyatı kaç TL dir?

Faiz Problemleri

Faiz problemlerinde kullanılacak terimler ve bu terimlerin kısalmaları aşağıdaki gibidir:

F: Faiz Miktarı
A:Ana para
n:Yıllık faiz yüzdesi
t: Süre(yıl, ay, gün)

Örnek:

Yıllık %30 faizle  bankaya yatırılan 2000 TL, 3 yılın sonunda  kaç lira faiz getirir?

Çözüm:

Karışım Problemleri

Karışım problemlerini ” karışıma giden madde miktarlarının toplamı son karışımdaki madde miktarına eşittir.” ifadesini formülleştirerek çözeriz.

Formül:

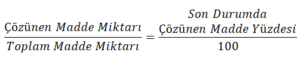
Ağırlıkça şeker oranı % x olan A gramlık bir karışımdaki şeker miktarı

Örnek:

150 gram şekerli suyun %12 si şeker olduğuna göre bu karşımda kaç gram su vardır?

Çözüm:

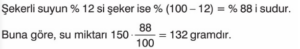
Örnek:

%20 si tuz olan  bir tuzlu su karışımındaki su miktarı tuz miktarından 60 gram fazla olduğuna göre, bu karışım kaç gramdır?

Çözüm:

TYT Matematik Konuları Konu Dağılımı için tıklayınız.

AYT Matematik Konuları Konu Dağılımı için tıklayınız.