Sayma ve Olasılık Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Sayma ve Olasılık konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Sayma ve Olasılık
Sıralama ve Seçme
Sayma Yöntemleri
Bire Bir Eşleme Yoluyla Sayma:
Bir kümenin eleman sayısını, verilen kümenin elemanları ile pozitif tam sayılar kümesinin elemanları arasında bire bir eşleme yaparak bulma işlemine bire bir eşleme yoluyla sayma denir.
Örnek
A = {1, 2, 3, 4, 5} kümesindeki rakamlar kullanılarak üç basamaklı
a. Kaç doğal sayı oluşturulabileceğini
b. Rakamları farklı kaç doğal sayı oluşturulabileceğini
c. Kaç çift doğal sayı oluşturulabileceğini
d. Rakamları farklı kaç çift doğal sayı oluşturulabileceğini bulalım.
Çözüm: a. her bir basamak için yazılabilecek rakam ve sayılar gösterilmiştir. Buna göre oluşturulabilecek üç basamaklı doğal sayıların sayısı, 5 . 5 . 5 = 5 3 = 125 olur.
b. Oluşturulacak üç basamaklı sayıların rakamlarının farklı olması istendiğinden her basamakta kullanılacak rakam sayısı gösterildiği gibi bir eksiltilir. Buna göre oluşturulabilecek rakamlar farklı üç basamaklı doğal sayların sayısı, 5 . 4 . 3 = 60 olur.
c. Çift doğal say oluşturulması istendiğinden birler basamağına 2 veya 4 rakam yazılabilir. Onlar ve yüzler basamaklarına rakamların tamam yazılabilir. Anlaşılacağı gibi oluşturulabilecek üç basamaklı çift doğal sayıların sayısı, 5 . 5 . 2 = 50 olur.
Toplama Yoluyla Sayma
Ayrık iki kümenin birleşiminin eleman sayısını toplama işlemi yaparak bulmaya, toplama yoluyla sayma yöntemi adı verilir. A ve B sonlu ve ayrık iki küme olmak üzere
s(A U B) = s(A) + s(B) dir.
Örnek
5 farklı pasta ve 6 farklı sütlü tatlı arasından 1 pasta veya 1 sütlü tatlı kaç farklı şekilde seçilir bulalım.
Pasta kümesine P dersek s(P) = 5, sütlü tatlı kümesine T dersek s(T) = 6 olur.
s(P ∪ T) = s(P) + s(T)
s(P ∪ T) = 5 + 6 = 11 buluruz.
Çarpma Yoluyla Sayma
Ayrık iki kümenin kesişiminin eleman sayısını çarpma işlemi yaparak bulmaya, çarpma yoluyla sayma yöntemi adı verilir.
m herhangi bir işlemin gerçekleşme yollarının sayısını, n de ikinci bir işlemin gerçekleşme yollarının sayısını göstersin. m yoldan birisi ile yapılan ilk işlemden sonra ikinci işlem n yolla yapılabiliyorsa bu iki işlem birlikte m.n yolla yapılabilir. Bu durum işlem sayısı arttığında da geçerlidir. Yani; A, B ve C boş olmayan ayrık birer küme olmak üzere,
** A ve B kümelerinden birer eleman seçerek oluşturulabilecek tüm sıralı ikililerin sayısı;
s(AxB) = s(A) . s(B)
** A, B ve C kümelerinden birer eleman seçilerek oluşturulacak tüm sıralı üçlülerin sayısı;
s(AxBxC) = s(A) . s(B) . s(C)
şeklinde çarpma işlemi ile bulunur.
Faktöriyel
1 den n ye kadar olan sayma sayılarının çarpımına n faktöriyel denir ve n! şeklinde gösterilir. Özel olarak sıfır faktöriyel bire eşittir. (0! = 1)
Bazı doğal sayıların faktöriyelleri
0! = 1
1! = 1
2! = 1.2 = 2
3! = 1.2.3 = 6
4! = 1.2.3.4 = 24
5! = 1.2.3.4.5 = 120
6! = 1.2.3.4.5.6 = 720
7! = 1.2.3.4.5.6.7 = 5040
NOT: n! aşağıdaki şekillerde de yazılabilir.
n! = n . (n − 1)!
n! = n . (n − 1) . (n − 2)!
Örnek
Anne, baba ve 3 çocuktan oluşan bir aile, anne ve baba yan yana olmak şartıyla kaç farklı biçimde sıralanabilir bulalım.
Anne ve baba her zaman yan yana olacağı için anne ile baba 1 kişi (A-B) gibi düşünülür.
A-B, Ç1, Ç2, Ç3 nesnelerinin sıralaması 4! biçimde gerçekleşir. Anne ve baba kendi aralarında da 2! (A-B, B-A) şeklinde yer değiştirebilir.
Sonuç olarak 4! . 2! = 24 . 2 = 48 sıralama yapılabilir.
Permütasyon
n ve r birer doğal sayı ve r ≤ n olmak üzere n elemanlı bir kümenin birbirinden farklı r tane elemanından oluşan dizilişlerin her birine n’nin r’li permütasyonu (dizilişi) denir.
Örnek:
A = {1, 2, 3} kümesinin ikili permütasyonlarını yazalım.
A kümesinin elemanlarını ikişerli seçerek sıralı ikili şeklinde yazarsak:
(1, 2), (1, 3), (2, 1), (2, 3), (3, 1) ve (3, 2) elde ederiz.
3 elemanlı bir kümenin ikili permütasyonlarının sayısı 6’dır.
Permütasyon Sayısı
n elemanlı bir kümenin r’li permütasyonlarının sayısı P (n, r) ile gösterilir.
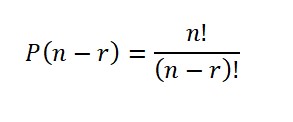
Örnek
7’nin 3’lü permütasyonlarının sayısını yani P (7, 3) değerini bulalım.
![]()
Permütasyon Özellikleri
1. n’nin sıfırlı permütasyonlarının sayısı
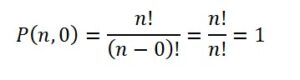
n’nin n’li permütasyonlarının sayısı
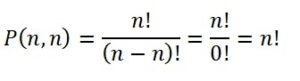
Tekrarlı Permütasyon
Bazı elemanları özdeş olan n elemanlı bir kümenin n’li permütasyonlarına tekrarlı permütasyon denir.

Kombinasyon
n ve r birer doğal sayı ve r ≤ n olmak üzere n elemanlı bir kümenin r elemanlı alt kümelerinin her birine n’nin r’li kombinasyonu denir.

Kombinasyonun Özellikleri

Pascal Üçgeni ve Binom Açılımı
Hintli matematikçiler ona Meru Dağı’nın merdivenleri der. İran’da Hayyam Üçgeni olarak bilinir. Çin’de ise Yang Hui’nin Üçgeni adı verilir. Batı dünyası da onu genelde Pascal Üçgeni olarak tanır.

Binom Açılımı
Bilinen özdeşlikler vardır bunlar;
(x + y)1 = x + y
(x + y)2 = (x + y).(x + y) = x2 + 2xy + y2
(x + y)3 = (x + y).(x + y).(x + y) = x3 + 3x2y + 3xy2 + y3
Kuvvet büyüdükçe özdeşliği çarpma işlemi yaparak bulmak zorlaşır. Bu durumda kombinasyon yardımıyla binom açılımını kullanarak özdeşlikleri bulabiliriz.
x ve y sıfırdan farklı ve n bir doğal sayı olmak (x + y)n ifadesinin x ve y’nin kuvvetleri cinsinden açılımına binom açılımı denir.
![]()
Binom açılımında terimleri oluştururken katsayıları kombinasyon yardımıyla hesaplarız. x’in azalan kuvvetlerine göre açılım yaparken x’in üssünü n’den başlayıp her terimde bir azaltırız, y’nin üssünü 0’dan başlayıp her terimde bir arttırırız. Böylece son terimde x’in üssü 0, y’nin üssü n olmuş olur.
Örnek
(x + y)4 ifadesinin özdeşini Pascal üçgeninden faydalanarak x’in artan kuvvetlerine göre yazalım.
Terimlerin katsayılarının 1 4 6 4 1 olduğunu Pascal üçgeninin 5. satırından görebiliriz. x’in kuvvetlerini 0’dan 4’e doğru, y’nin kuvvetlerini 4’ten 0’a doğru sırayla terimlere yazarız.
(x + y)4 = 1 x0 y4 + 4 x1 y3 + 6 x2 y2 + 4 x3 y1 + 1 x4 y0
Katsayılardaki 1’leri, x0 ve y0 ifadelerini 1’e eşit oldukları için yazmamıza gerek yoktur.
(x + y)4 = y4 + 4 x y3 + 6 x2 y2 + 4 x3 y + x4
Binom Açılımı Özellikleri
Terim sayısı
(x+y)n ifadesinin açılımındaki terim sayısı n+1‘dir.
Örnek: (2x + 3y)10 ifadesinin açılımında 10+1 = 11 terim vardır.
Terimlerdeki üsler toplamı
(x+y)n ifadesinin açılımındaki her bir terimdeki x ve y değişkenlerinin üsleri toplamı n‘dir.
Örnek: (3x − y)8 ifadesinin x’in azalan kuvvetlerine göre açılımındaki baştan 7. terimi inceleyelim.
Bu ifadenin açılımdaki 7. terimi 252x2y6 dir. Burdaki x’in ve y’nin üslerini toplarsak 2 + 6 = 8 olduğunu görürüz.
Baştan r+1 inci terim
(x+y)n ifadesinin x’in azalan kuvvetlerine göre açılımındaki baştan r + 1‘inci terim ![]()
Sondan r+1 inci terim
(x+y)n ifadesinin x’in azalan kuvvetlerine göre açılımındaki sondan r + 1‘inci terim ![]()
Ortanca terim
n doğal sayı olmak üzere (x+y)2n ifadesinin açılımındaki ortadaki terim ![]()
Katsayılar toplamı
(x+y)n ifadesinin açılımındaki katsayılar toplamını bulmak için değişkenler yerine 1 sayısı yazılır.
Sabit terim
(x+y)n ifadesinin açılımındaki sabit terimi bulmak için değişkenler yerine 0 sayısı yazılır.
Basit Olayların Olasılıkları
Olasılık hem günlük hayatta hem de değişik bilim dallarında çok sık kullanılır. Bugün olasılığın ekonomi, meteoroloji, temel bilimler, milli savunma, vb. birçok uygulama alanı vardır.
Deney: Bir olayın sonucunun ne olacağını görmek için yapılan işleme deney denir.
Çıktı: Deneyin sonucunda elde edilebilecek sonuçlara çıktı denir.
Örnek Uzay: Bir deneyde elde edilebilecek tüm çıktıların kümesine Örnek uzay denir ve E ile gösterilir.
Örnek Nokta: Ömek uzayın herhangi bir elemanına örnek nokta denir.
Örnek:
Madeni bir paranın havaya atılması deneyinde, para yere düşmeden kesin olarak yazı mı, tura mı geleceğini bilemeyiz.
Bu deneyin çıktıları yazı veya turadır. Yazıyı Y, turayı T harfi ile gösterirsek, tüm çıktıların oluşturduğu küme örnek uzay olacağı için E = {Y, T} olur. Yazı gelmesi ya da tura gelmesi ise bir olaydır.
İmkansız Olaylar: Gerçekleşmesi mümkün olmayan olaylar,
Bir zarın atılması deneyinde üst yüze gelen sayının 6 dan büyük olması gerçekleşmesi mümkün olmayan olaydır.
Kesin Olaylar: Gerçekleşmesi kesin olan olaylardır,
Sadece erkeklerin bulunduğu bir sınıftan seçilen öğrencinin erkek olma olayı kesin olaydır.
Eşit Olasılıklı Olaylar: Bir zarın havaya atılması deneyinde üst yüze birden altıya kadar olan sayıların gelmesi eşit olasılıklı olaydır.
Bir madeni para atıldığında yazı ve tura gelme olasılığı birbirine eşittir.
Daha Fazla Olasılıklı Olaylar: 10 tane kız 5 tane erkek bulunan bir sınıftan seçilen öğrencinin kız olma olasılığı daha fazladır.
Daha Az Olasılıklı Olaylar : 40 tane kırmızı 2 tane mavi top bulunan bir torbadan seçilen topun mavi olma olasılığı daha azdır.







İyi di umarım hoca. Memnun olurum 🙂
Güzeldi işime yaradı
Güzel bir ödev ama bazı bölümlerde yazım hataları ve eksik bölümler var
Süper teşekkürler
çok işime yaradı teşekkürler 🙂