Trigonometri Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Trigonometri konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Trigonometri
- Yönlü Açılar
- Trigonometrik Fonksiyonlar
- Trigonometrik Özdeşlikler
- Kosinüs Teoremi ve Sinüs Teoremi
- Trigonometrik Fonksiyonların Periyotları
- Trigonometrik Fonksiyonların Grafikleri
- Ters Trigonometrik Fonksiyonlar
Yönlü Açılar
Bir açının iki tane kenarı vardır. Bunlardan birisi başlangıç diğeri ise bitim kenarıdır. Başlangıç ve bitim kenarına göre açının yönü değişir.
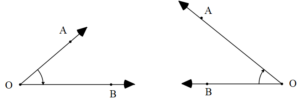
Saatin dönme yönünün tersi olan yöne pozitif yön, aynı olan yöne negatif yön denir.
Merkez Açı nedir?
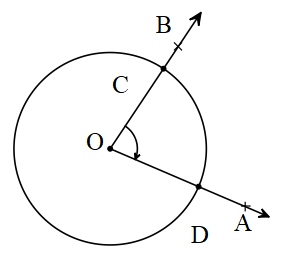
İki yarıçapın oluşturduğu açıya merkez açı denir. Merkez açının ölçüsü gördüğü yayın ölçüsüne eşittir.
Açı Ölçü Birimleri
Açının kenarları arasındaki açıklığa açı denir ve bir açının büyüklüğünü ve küçüklüğünü ifade etmek için bazı açı ölçü birimlerini kullanırız. Yaygın olarak kullandığımız açı ölçme birimleri derece ve radyandır.
Derece: Çember yayının 360 eşit yay parçasına bölenmesiyle elde edilen parçalardan her birini gören merkez açının ölçüsü 1 derece dir.
– Tam çember yayının ölçüsü 360° dir.
– 1 derece 60 dakikaya eşittir. 1° = 60′
– 1 dakika 60 saniyeye eşittir. 1′ = 60″
Grad: Dairenin 400 eşit parçaya bölünmüş yaylarından birine 1 grad denir. Buna göre bir dairenin tüm yaylarının ölçüsü 400 graddır.
Radyan: Bir dairede, yarı çapı uzunluğundaki bir yayı gören merkez açının ölçüsüne 1 radyan denir. 1 radyan 57.2957795 derecedir.
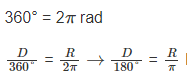
Birim Çember: Birim Çember, yarıçapı 1 cm, merkezi orijin (0,0) olan çembere verilen isimdir.
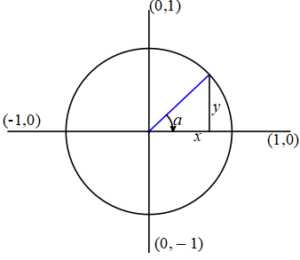
cosα Açı α dereceyken mavi doğru parçasının çemberi kestiği notanın x değeridir.
sinα Açı α dereceyken mavi doğru parçasının çemberi kestiği noktanın y değeridir.
Esas Ölçü: Esas ölçü, açının 0° ile 360° arasındaki ölçüsüne denir.
-180° = π
-90° = π/2
-360° = 2π
360°’den büyük açının esas ölçüsünü bulma: Verilen sayıyı 360’a böleriz, kalan sayı bize esas ölçüyü verecektir.
0°’den küçük açının esas ölçüsünü bulma: Verilen sayı işareti önemsenmeden yine 360’a bölünür ve kalan sayı 360’tan çıkarılır.
π cinsinden verilen açının esas ölçüsünü bulma: Sayının yaklaşık değerini bulup içerisinden 2π ve katlarını(4π,6π,8π…) çıkaracağız.
π cinsinden negatif verilen açıların esas ölçüsünü bulma: Sayının yaklaşık değeri bulup sayıyı en küçük pozitif yapacak 2π ve katlarını (4π,6π,8π…) sayıya ekleriz.
Trigonometrik Fonksiyonlar
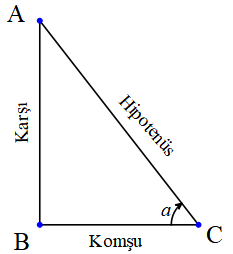
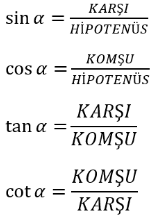
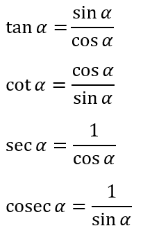
![]()
Sinüs Fonksiyonu
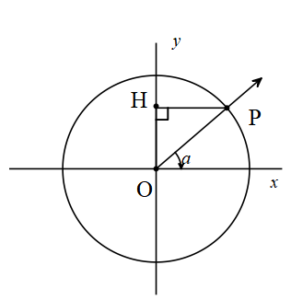
a açısının bitim kenarının birim çemberi kestiği P noktasının koordinatları (x,y) olmak üzere P noktasının ordinatına a açının sinüsü denir.
y=sina şeklinde gösterilir. a açısını sina yapan fonksiyona sinüs fonksiyonu denir.
![]() formülü ile bulunur.
formülü ile bulunur.
Kosinüs Fonksiyonu
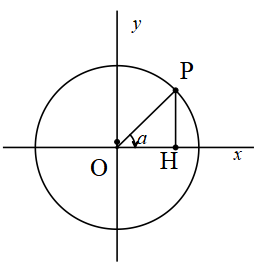
a açısının bitim kenarının birim çemberi kestiği P noktasının koordinatları (x,y) olmak üzere P noktasının apsisine a açının kosinüsü denir.
x=cosa şeklinde gösterilir. a açısını cosa yapan fonksiyona kosinüs fonksiyonu denir.
Tanjant Fonksiyonu
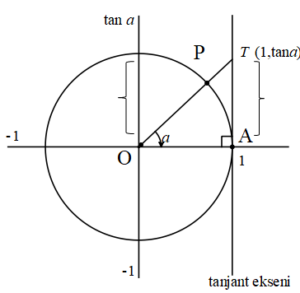
Bir a açısının bitim kolunun x=1 doğrusu ile kesiştiği T noktasının ordinatına a açısının tanjantı denir. tana ile gösterilir.
a reel sayısını tana ile eşleştiren fonksiyona tanjant fonksiyonu denir.
![]() olduğunda a’nın bitim kolu tanjant eksenine (x=1 doğrusuna) paralel olacağından
olduğunda a’nın bitim kolu tanjant eksenine (x=1 doğrusuna) paralel olacağından ![]() tanımsızdır.
tanımsızdır.
Kotanjant Fonksiyonu
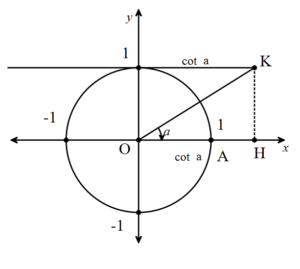
Bir a açısının bitim kolunun Y=1 doğrusu ile kesiştiği T noktasının ordinatına a açısının kotanjantı denir. cota ile gösterilir.
a reel sayısını cota ile eşleştiren fonksiyona kotanjant fonksiyonu denir.
a=0º,a=180ºa=360º için açının bitim kolu Y=1 doğrusuna paralel olduğundan kesişmezler. O yüzden cot 0º,cot πº,cot 2πº tanımsızdır.
Sekant Fonksiyonu
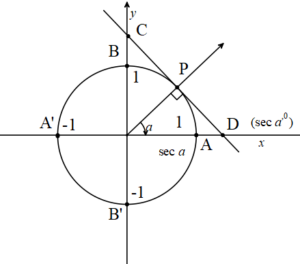
a açısının çemberi kestiği P noktasından çizilen teğetin x eksenini kestiği D noktasının apsisine a açısının sekantı denir ve sec a ile gösterilir. a=90º ve a=270º için teğet ler x eksenine paralel olduğundan x eksenini kesmezler o yüzden sec90º ve sec270º tanımsızdır.
Trigonometrik Özdeşlikler

Kosinüs Teoremi ve Sinüs Teoremi
Kosinüs Teoremi
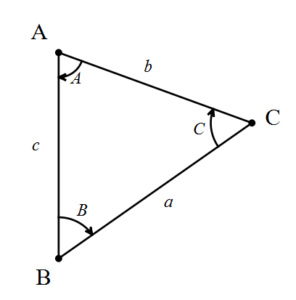
a2 = b2 + c2 – 2.b.c.cosA◦
b2 = a2 + c2 – 2.a.c.cosB◦
c2 = a2 + b2 – 2.a.b.cosC◦
Kosinüs Teoreminin İspatı
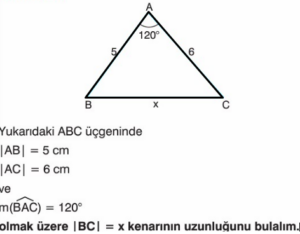

Çözüm

Sinüs Teoremi
ABC üçgeninin çevrel çemberinin merkezi O ve yarıçapı R olmak üzere;
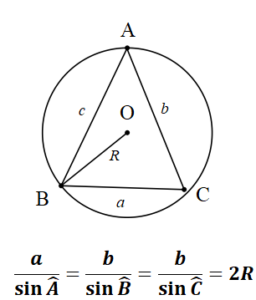
Sinüs Teoreminin İspatı
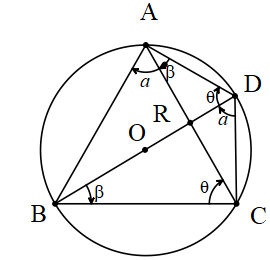
ABC üçgeninin çevrel çemberinin yarıçapı olan [BO] kenarını doğrultusunu bozmadan uzatalım. Çemberi kestiği noktaya D diyelim [BD] çemberinin çapı olur A köşes ile D noktasını birleştirelim. BAD açısı 90º olur.
a+β=90º
Aynı yayı gören çevre açıları eşittir.
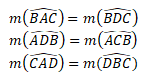 dir.
dir.
DBC üçgeninde a açısının sinüs değerine bakılırsa
![]()
Trigonometrik Fonksiyonların Periyotları
Periyot: Bir fonksiyonun tanım kğmesindeki bir x sayısı için f(x+T)=f(x) olarak sıfırdan farklı en az bir T sayısı varsa bu T sayısına f fonksiyonunun periyodu denir.
f(x-T)=f(x) eşitliğini sağlayan birden fazla T€R varsa bunların içindeki en küçük pozitif T sayısına f fonksiyonun esas periyodu denir.
İki fonksiyonun toplamının periyodu f’nin periyodu Tf g’nin periyodu Tg ise f+g’nin periyodu Okek(Tf,Tg) olur.
Sinüs ve Kosinüs Fonksiyonlarının Periyodu
a,b,c,d € R a≠0 m € Z+ olmak üzere f(x)=c+dsinm (ax+b)ve g(x)=c+dcosm (ax+b) fonksiyonlarının periyodu (esas periyodu),
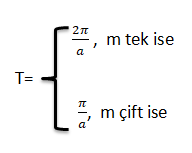
Tanjant ve Kotanjant Fonksiyonlarının Periyodu
a,b,c,d € R , a≠0 m € Z+ olmak üzere f(x)=c+dtanm (ax+b) ve g(x)=c +dcotm(ax+b) fonksiyonlarının (esas) periyodu
![]()
Trigonometrik Fonksiyonların Grafikleri
sinx Fonksiyonunun Grafiği
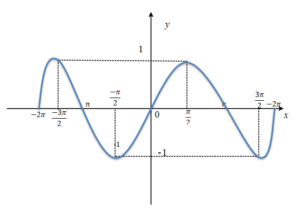
sinx fonksiyonun [-2π,2π] aralığında grafiği yukarıdaki gibidir.
cosx Fonksiyonunun Grafiği
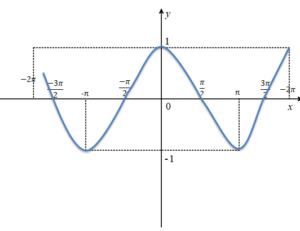
cosx fonksiyonun [-2π,2π] aralığında grafiği yukarıdaki gibidir.
tanx Fonksiyonunun Grafiği
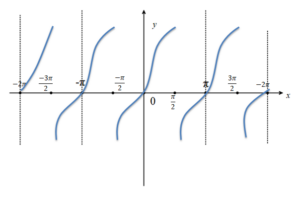
tanx fonksiyonun [-2π,2π] aralığında grafiği yukarıdaki gibidir.
cotx Fonksiyonunun Grafiği
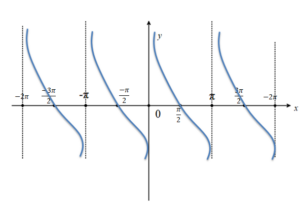
cotx fonksiyonun [-2π,2π] aralığında grafiği yukarıdaki gibidir.
Ters Trigonometrik Fonksiyonlar
Arcsin Fonksiyonu

Arccos Fonksiyonu

Arctan Fonksiyonu

Arccot Fonksiyonu








🤍🤍🤍