Türevin Uygulamaları Konu Anlatımı

Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak bilgi sahibi olabilirsiniz. Türevin Uygulamaları konusu ile ilgili bütün soruların cevabı sizleri bekliyor…
Türevin Uygulamaları
- Bir Fonksiyonun Artan veya Azalan Olduğu Aralıklar
- Bir Fonksiyonun Yerel Maksimum ve Yerel Minimum ile Mutlak Maksimum ve Mutlak Minimum Noktaları
- Türev Yardımıyla Bir Fonksiyonun Grafiğinin Çizimi
- Maksimum ve Minimum Problemleri
Bir Fonksiyonun Artan veya Azalan Olduğu Aralıklar




Bir Fonksiyonun Yerel Maksimum ve Yerel Minimum ile Mutlak Maksimum ve Mutlak Minimum Noktaları





Yukarıda grafiği verilen fonksiyonların ![]() noktaları yerel maksimum noktalarıdır.
noktaları yerel maksimum noktalarıdır.



Yukarıda grafiği verilen fonksiyonların ![]() noktaları yerel minimum noktalarıdır.
noktaları yerel minimum noktalarıdır.
Bir fonksiyonun yerel maksimum ve yerel minimum noktalarına genel olarak ekstremum
noktaları denir.
Bir fonksiyonun tanımlı olduğu aralıktaki en büyük değerini aldığı noktaya mutlak maksimum noktası, en büyük değerine ise mutlak maksimum değeri denir.
Bir fonksiyonun tanımlı olduğu aralıktaki en küçük değerini aldığı noktaya mutlak minimum noktası, en küçük değerine ise mutlak minimum değeri denir.
Bir fonksiyonun azalanlıktan artanlığa geçtiği noktaya yerel minimum noktası denir.
Bir fonksiyonun artanlıktan azalanlığa geçtiği noktaya yerel maksimum noktası denir.
Türev Yardımıyla Bir Fonksiyonun Grafiğinin Çizimi
Bir fonksiyonun grafiği çizilirken tanım kümesine dikkat edilmelidir. Bu bölümde yalnızca
polinom fonksiyonlarının grafikleri çizileceğinden polinom fonksiyonlarının en geniş tanım kümesi olan gerçek sayılar kümesinde grafik çizimi yapılacaktır.
Fonksiyonun eksenleri kestiği noktalara bakılmalıdır. f] gx = 0 denkleminin tek katlı köklerinde grafik x eksenini keserken çift katlı köklerinde x eksenine teğet olacaktır.
Fonksiyonun türevi yardımıyla varsa ekstremum noktaları bulunmalı ve artan ile azalanlık durumları incelenmelidir.

fonksiyonun grafiği

Maksimum ve Minimum Problemleri
Bir problemde bir ifadenin alabileceği maksimum (veya minimum) değer soruluyorsa öncelikle bu ifadeyi bir fonksiyon olarak ifade etmemiz gerekir. Daha sonra bu fonksiyonun maksimum (veya minimum) değerini bulmak için bu fonksiyonun birinci türevi sıfıra eşitlenir. Oluşan bu denklemdeki köklere göre birinci türevin işaret tablosu yapılıp maksimum (veya minimum) değer bulunur.
Örnek 1:
Duygu ve kardeşi Uğur, harçlıklarını harcamayıp biriktirerek Anneler Günü hediyesi almak istiyorlar. Duygu’nun günlük harçlığı x TL ve Uğur’un günlük harçlığı y TL dir. Duygu tüm harçlığını 3y gün ve Uğur ise tüm harçlığını 3x gün biriktiriyor. Duygu’nun 2 günlük harçlığı ile Uğur’un 3 günlük harçlığının toplamı 24 TL dir. Biriken toplam paranın en fazla olabilmesi için Duygu ve Uğur’un günlük harçlıklarının kaç TL olması gerektiğini bulunuz.
Çözüm:
Duygu’nun günlük harçlığı x TL olup 3y günde 3xy TL para biriktirir. Uğur’un günlük harçlığı y TL olup 3x günde 3xy TL para biriktirir. Bu durumda biriken toplam para olan 6xy TL nin maksimum olmasını sağlayan x ve y değerleri bulunmalıdır. Duygu’nun 2 günlük harçlığı ile Uğur’un 3 günlük harçlığının toplamı 24 TL olduğundan
2x+3y= 24 olur.

Bu durumda 6xy ifadesi ![]() fonksiyonu ile ifade edilirse 6xy ifadesinin en büyük olması için
fonksiyonu ile ifade edilirse 6xy ifadesinin en büyük olması için ![]() fonksiyonunu maksimum yapan x değeri bulunmalıdır.
fonksiyonunu maksimum yapan x değeri bulunmalıdır.
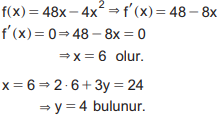
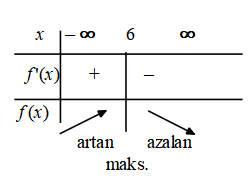
Buna göre Duygu ve Uğur’un günlük harçlıklarının sırasıyla 6 TL ve 4 TL olması durumunda biriken toplam para en fazla olacaktır.
Örnek 2:

Bir kişi evinin bahçesi için aldığı 16 metre tel ile şekildeki gibi bir duvar olan dikdörtgen biçimde bir kümes yapacaktır. Bu kümesin alanının en fazla kaç metrekare olacağını bulunuz.
Çözüm:


Bu durumda ABCD dikdörtgeninin alanı ![]() fonksiyonu ile ifade edilirse ABCD dikdörtgeninin alanının en çok olması için
fonksiyonu ile ifade edilirse ABCD dikdörtgeninin alanının en çok olması için ![]() fonksiyonunun maksimum değeri bulunmalıdır.
fonksiyonunun maksimum değeri bulunmalıdır.
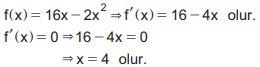

f(x) fonksiyonunun türevinin işaret tablosu incelenirse fonksiyonun maksimum değerini x =4 için aldığı görülür. Bu durumda fonksiyonun maksimum değeri f(4) olup bu değer

O hâlde kümesin alanı en fazla 32 metrekare bulunur.
Örnek 3:
![]() fonksiyonunun grafiği üzerindeki bir (a,b) noktasının koordinatları toplamının alabileceği en küçük değeri bulunuz.
fonksiyonunun grafiği üzerindeki bir (a,b) noktasının koordinatları toplamının alabileceği en küçük değeri bulunuz.

12. Sınıf Matematik Konuları için tıklayınız
12. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız.






