Merhaba arkadaşlar size bu yazımızda Matematik Konuları hakkında bilgi vereceğiz. Yazımızı okuyarak  bilgi sahibi olabilirsiniz. Üçgenlerin Yardımcı Elemanları konusu ile ilgili bütün soruların cevabı sizleri bekliyor…

Üçgenlerin Yardımcı Elemanları

• Açıortay
• Kenarortay
• Orta Dikme
• Yükseklik

Açıortay

Bir açıyı iki eş açıya ayıran ışına açıortay denir. Açıortay iç ve dış açıortay olmak üzere ikiye ayrılır.

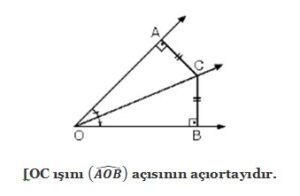
Açıortay Teoreminin İspatı

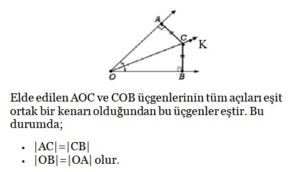
Üçgende İç Açıortay

Bir üçgenin bir iç açısını iki eş açıya ayıran ışına o üçgenin iç açıortayı denir. Bir üçgende iç açıortaylar tek noktada kesişir.

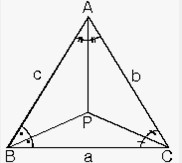
Bir üçgende iç açıortayların kesişim noktası üçgenin iç teğet çemberinin merkezidir.

Üçgende İç Açıortay Teoremi

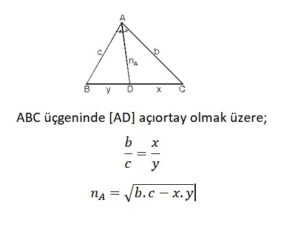
Üçgende Dış Açıortay 

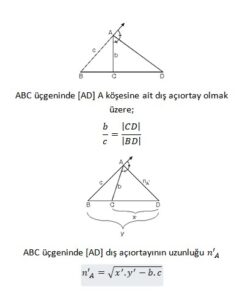
Kenarortay

Bir üçgende bir köşeyi karşısındaki kenarın orta noktasına birleştiren doğru parçasına o kenara ait kenarortay denir.

1. Üçgenlerde kenarortaylar bir noktada kesişirler. Kenarortayların kesişim noktasına ağırlık merkezi denir.

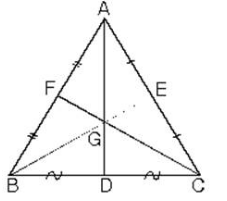
ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarının kesiştikleri G noktasına ABC üçgeninin ağırlık merkezi denir.

Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim uzaklık olacak şekilde böler.

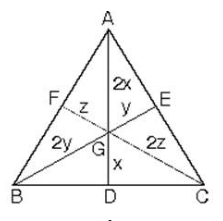
ABC üçgeninde D, E, F noktaları bulundukları kenarların orta noktaları ve G ağırlık merkezi ise

|AG|=2|GD|
|BG|=2|GE|
|CG|=2|GF|

Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.

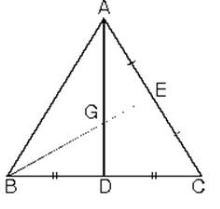
ABC üçgeninde [AD] kenarortay ve |AG| = 2|GD| olduğunda G noktası ağırlık merkezidir.

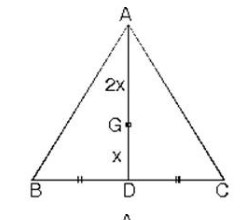
ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG| olduğunda G noktası ağırlık merkezidir.

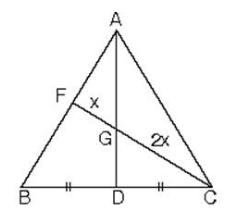
ABC üçgeninde |AG| = 2|GD| ve |CG| = 2|GF| eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.

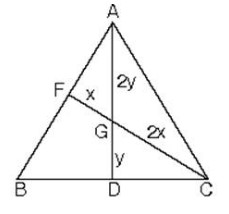
2. Dik üçgende hipotenüse ait kenarortay (dik köşeden çizilen kenarortay) hipotenüsün yarısına eşittir.

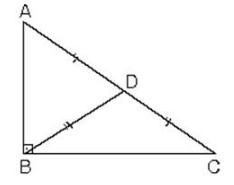
ABC dik üçgeninde [BD] hipotenüse ait kenarortay |AD|=|DC|=|BD|

3. Kenarortayların Böldüğü Alanlar

Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.

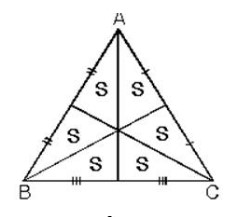
G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

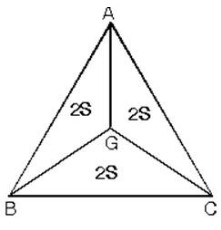
G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.

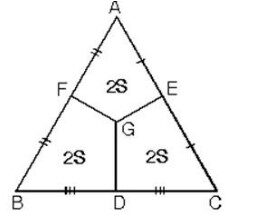
4. ABC üçgeninde kenarortaylar ve orta taban [FE] çizilirse

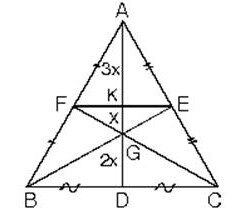
|AK| = 3x
|KG| = x
|GD| = 2x eşitlikleri bulunur.

Bu kuran 312 kuralı olarak da adlandırabilir.

K noktası [AD] kenarortayının orta noktasıdır. Ayrıca [FE] orta taban olduğundan;

[FE] // [BC] 2[FE]=[BC]

ABC üçgeninde kenarortaylar ve [FE] çizildiğinde şekildeki gibi bir alan bölünmesi oluşur.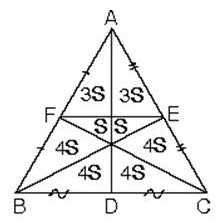

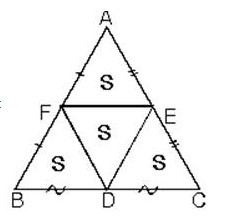
Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.

5. Kenarortay Uzunluğu (Kenarortay Teoremi)

ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğu V_a ;

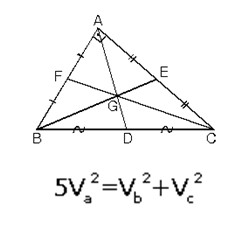
6. Dik Üçgende Kenarortaylar

A açısı 90° olan bir dik üçgende kenarortaylar arasında

Orta Dikme

Bir doğru parçasının orta noktasından geçen ve doğru parçasına dik olan doğruya orta dikme doğrusu denir.

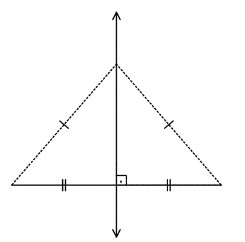
Orta dikmenin noktanın üstündeki herhangi bir noktadan, doğru parçasının uç noktalarına olan uzaklıklar birbirine eşittir.

Üçgende Kenar Orta Dikme

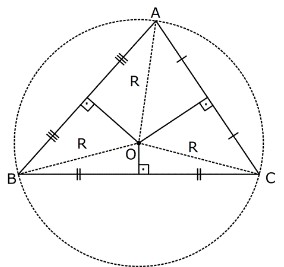
Üçgenin kenar orta dikmeleri O noktasında kesiştiğinden 0 noktası, ABC üçgeninin çevrel çemberinin merkezidir
[OA], [OB] ve [OC] çevrel çemberin yarıçaplarıdır.
|OA|=|OB|=|OC|=r olur.

Yükseklik

Üçgenin bir köşesinden karşısındaki kenara çizilen dikmeye üçgenin o kenarına ait yüksekliği denir. Yükseklik daima kenara diktir.

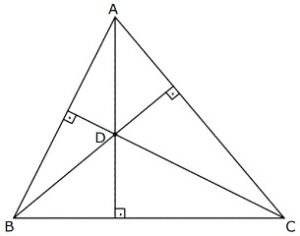
Bir üçgende yükseklikler tek bir noktada kesişir. Bu noktaya da diklik merkezi denir.

İkiz Kenar Üçgende Yükseklik

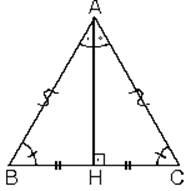
İkizkenar üçgenlerde eşit olmayan kenara indirilen dikme üçgeni iki eş üçgene ayırır.

1. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.

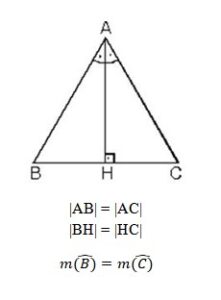
2. Bir üçgende, açıortay aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.

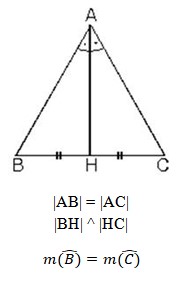
3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.

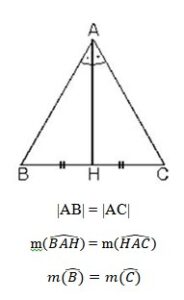
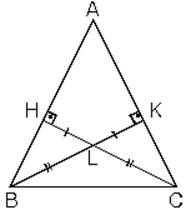
4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.

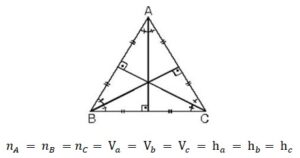
Eşkenar Üçgende Yükseklik

1. Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir.

2. Eşkenar üçgenin bir kenarına a dersek yükseklik;

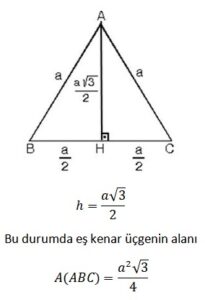
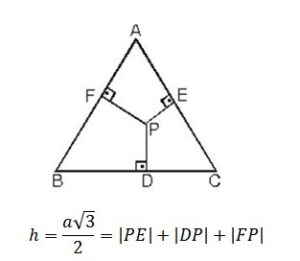
3. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende;

9. Sınıf Matematik Konuları için Tıklayınız

9. Sınıfta Yer Alan Diğer Ders ve Konuları için Tıklayınız